Homeostatic controllers compensating for growth and perturbations

Abstract

Cells and organisms have developed homeostatic mechanisms which protect them against a changing environment. How growth and homeostasis interact is still not well understood, but of increasing interest to the molecular and synthetic biology community to recognize and design control circuits which can oppose the diluting effects of cell growth. In this paper we describe the performance of selected negative feedback controllers in response to different applied growth laws and time dependent outflow perturbations of a controlled variable. The approach taken here is based on deterministic mass action kinetics assuming that cell content is instantaneously mixed. All controllers behave ideal in the sense that they for step-wise perturbations in volume and a controlled compound A are able to drive A precisely back to the controllers’ theoretical set-points. The applied growth kinetics reflect experimentally observed growth laws, which range from surface to volume ratio growth to linear and exponential growth. Our results show that the kinetic implementation of integral control and the structure of the negative feedback loop are two properties which affect controller performance. Best performance is observed for controllers based on derepression kinetics and controllers with an autocatalytic implementation of integral control. Both are able to defend exponential growth and perturbations, although the autocatalytic controller shows an offset from its theoretical set-point. Controllers with activating signaling using zero-order or bimolecular (antithetic) kinetics for integral control behave very similar but less well. Their performance can be improved by implementing negative feedback structures having repression/derepression steps or by increasing controller aggressiveness. Our results provide a guide what type of feedback structures and integral control kinetics are suitable to oppose the dilution effects by different growth laws and time dependent perturbations on a deterministic level.

Introduction

The term homeostasis was defined by Walter B. Cannon [1] to describe the coordinated ability of organisms and cells to maintain an internal stability by keeping concentrations of cellular components within certain tolerable limits [2]. Cannon’s emphasis on homeo indicates that he considered the internal physiological state not as a constant, as suggested earlier by Bernard’s concept of a fixed “milieu intérieur” [2, 3], but conceives homeostasis as a dynamic adaptable system which allows variations within certain limits. Dependent on the controlled components, the homeostatic limits in which one or several controllers operate can vary considerably. For example, while the negative feedback regulation of cellular sodium shows an apparently changing and less well-defined set-point [4, 5], the regulation of other metal ions have more strict limits [6–8].

Growth, an essential aspect of all living beings is a highly regulated process. According to Bertalanffy [9, 10], the different observed growth kinetics of organisms can be related to the organisms’ metabolism. For example, when respiration is proportional to the surface of the organism linear growth kinetics are obtained. On the other hand, if respiration is proportional to the organism’s weight/volume, exponential growth occurs. Growth kinetics of bacteria [11, 12] appear closely related to the bacterial form or shape. Rod-shaped bacteria show exponential growth rates, i.e.

$$\begin{array}{c}\hfill \dot{V}=\kappa V;\kappa >0\end{array}$$ (1)

whereas spherical bacteria increase their cellular volume by a rate law related to the surface to volume ratio, i.e.,

$$\begin{array}{c}\hfill \dot{V}=\eta ·V^{\frac{2}{3}}-\xi ·V\end{array}$$ (2)

where η and ξ are constants reflecting anabolism and catabolism, respectively [13].

Although the protective functions of homeostasis need to be in place during growth, the interacting mechanisms between homeostasis and growth are not well understood. In principle, there are two aspects of growth to consider. The first one, which is focused on in this paper is how homeostatic mechanisms can compensate for growth without affecting it. The second aspect, which will be treated in another paper, is how homeostatic mechanisms can influence growth. In this paper we consider growth as an increase of the cellular volume. As a continuous process growth represents a time-dependent perturbation which would lead to the dilution of cellular/cytosolic compounds unless other mechanisms counteract for it.

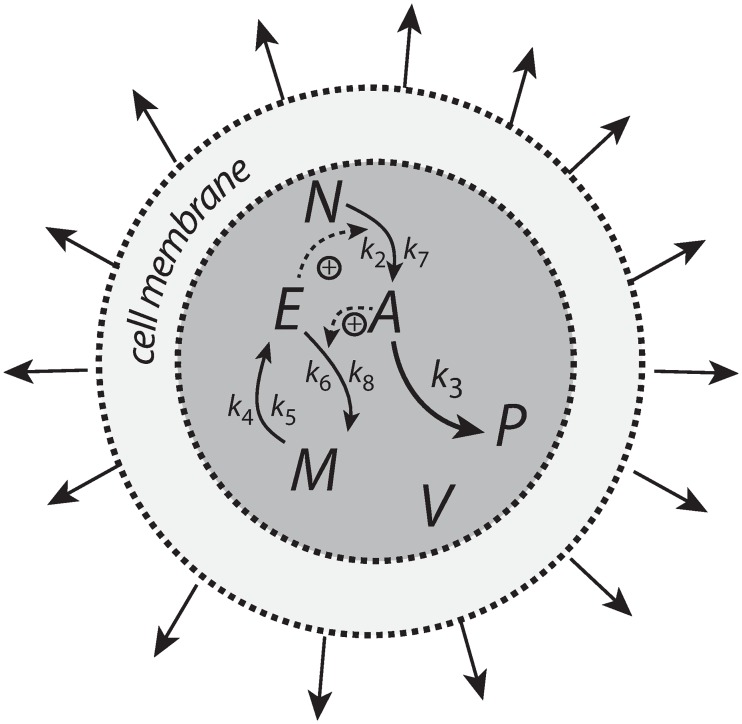
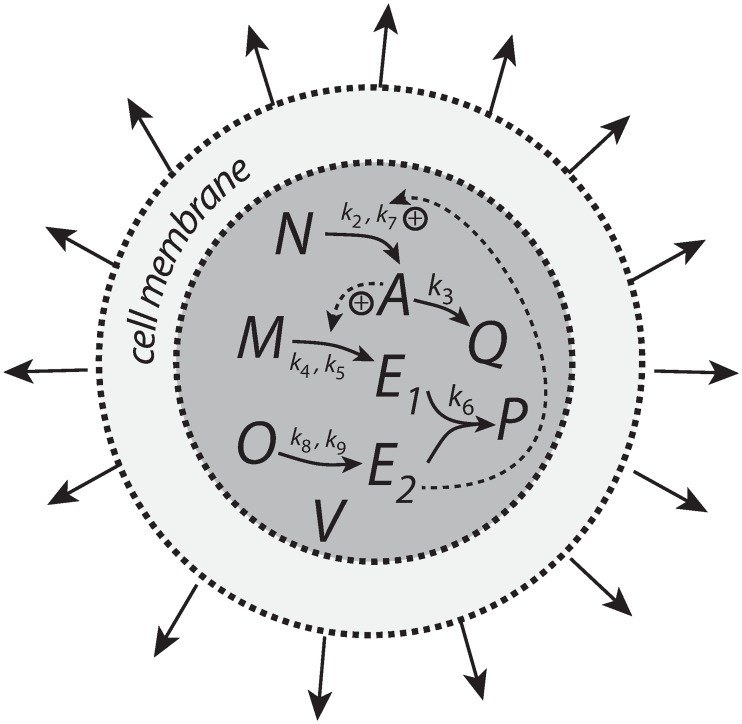
Integral control is a concept from control engineering [14], which enables robust regulation for step-wise perturbations and has been implicated to occur in a variety of homeostatic regulated systems [5, 15–17]. How different integral controllers will perform under (nonlinear) time-dependent growth is little investigated. Based on a previous study [18] we have chosen four controller motifs, which are shown in Fig 1. The most promising controllers which are able to handle nonlinear time dependent growth are a motif 2 zero-order type of controller based on derepression and a motif 1 first-order controller based on autocatalysis [19–21]. A relatively new discovered integral feedback mechanism, the so-called antithetic motif [22], has also been included. For comparison, we have also included a motif 1 zero-order type of controller. The controllers were investigated with respect to their capabilities to compensate for time-dependent outflow perturbations in A and in the presence of different growth laws (increase in the reaction volume V) according to Bertalanffy’s classifications [9, 10]. The growth kinetics that will be considered include linear (constant) as well as saturating and exponential growth laws. We focus here primarily on outflow perturbations, because together with the diluting effects of the different growth laws these perturbations represent the most severe conditions for testing the controllers.

Fig 1. The controllers investigated in this study.

Reaction orders are with respect to E. The reaction between E₁ and E₂ in the antithetic controller is an overall second-order process. The controllers behave ideal in the sense that they for step-wise changes in A and/or V, are able to keep A precisely at their defined theoretical set-points $A_{set}^{theor}$.

Materials and methods

To arrive at controller candidates which can oppose various dilution and perturbation kinetics a couple of simplifications have been made, which are discussed in more detail below. One is the assumption that compounds in a growing cells undergo instantaneous and ideal mixing, thereby ignoring the spatial organization of the cell. In addition, we ignore stochastic effects due to diffusion or low molecule numbers (however, see Discussion). Deterministic computations were performed by using the Fortran subroutine LSODE [23]. Plots were generated with gnuplot (www.gnuplot.info) and Adobe Illustrator (adobe.com). To make notations simpler, concentrations of compounds are denoted by compound names without square brackets. Time derivatives are generally indicated by the ‘dot’ notation. Concentrations and rate parameter values are given in arbitrary units (au). Rate parameters are presented as k_i’s (i = 1, 2, 3, …) irrespective of their kinetic nature, i.e. whether they represent turnover numbers, Michaelis constants, or inhibition constants. A set of MATLAB (mathworks.com) calculations with instructions are provided in the Supporting Information as a combined zip-file (S1 Matlab).

Overview of treated cases and analytical steady state expressions

The four controller motifs are studied for internal and transporter-based compensatory fluxes, different growth laws, and different removal kinetics of the controlled variable A. In the following we give a brief summary how the paper is structured and under what conditions the four motifs are tested. The paper divides into the following major parts.

In chapter “Reaction kinetics during volume changes” the rate equations during volume changes are derived.

The results are divided into two major cases:

In Case A: “Controllers with transporter-based compensatory fluxes” the behaviors of the four negative feedback motifs are shown when the compensatory fluxes are transporter based and when systems are exposed to linear and exponential growth with corresponding removal kinetics in A during growth. The transporter-based compensatory fluxes consist of an (by controller molecule E activated or derepressed) zero-order inflow of A molecules with respect to the transporter, $\dot{n_A}$, which for each time point is divided by the volume to get the contribution to the concentration of A due to the inflow.

In Case B: “Controllers with cell-internal compensatory fluxes” results are described when the compensatory fluxes are generated cell-internally and when the systems are exposed to linear, exponential, and surface-to-volume ratio related growth. Also here, during growth, A is subject to linear and exponential removal kinetics.

For most of the numerically studied control structures analytical steady state expressions for A are derived in the Supporting Information. The analytical expressions in A_ss are derived by writing first down the rate equations for A and E (E₁ and E₂ for the antithetic controller), while treating fluxes coming from precursor species as constants, i.e., rates are zero-order with respect to these species. Then the second time-derivative Ä is calculated and the rate equation of E (E₂ for the antithetic controller) is inserted into the Ä equation which is set to zero. This leads to an analytical expression for A_ss showing how different parameters influence the steady state.

In “Overview of results” the four motifs are ranked according to their abilities to oppose the different growth laws and outflow perturbations. The motif 2 based controller with repression/derepression kinetics clearly outperforms the other motifs, followed by the autocatalytic motif 1 controller. The performance of the four motifs is discussed in terms of the internal model principle, which reflects the kinetic limits controllers can handle.

We also demonstrate the influence the feedback structure (termed motifs in [7]) has in relationship with the integral controller part. Using an antithetic integral controller together with a motif 2 repression/derepression structure as an example, we show how the motif 2 structure improves controller performance, but also point to the limitations which are caused by the kinetics of the integral controller.

Reaction kinetics during volume changes

To describe concentration changes during cell growth we have to consider the concentration changes due to the increasing reaction volume V. If A denotes the concentration of n_A moles of compound A in volume V, the overall change of concentration A is composed of two terms, one that describes the changes of A while V is kept constant, ${\left(\dot{A}\right)}_V$, and of a second term, $A(\dot{V}/V)$, which describes the influence of the volume changes on the concentration of A, i.e.,

$$\begin{array}{c}\hfill \dot{A}=\frac{\dot{n_A}}{V}-A\left(\frac{\dot{V}}{V}\right)={\left(\dot{A}\right)}_V-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (3)

Eq 3 will be used as a “template” when formulating the rate equations of cellular compounds in the presence of changing V. Before we turn to the actual controller examples we show how growth ($\dot{V}$) affects the concentration of a given species A (which will be later our controlled variable) when A is unreactive, being produced internally within the cell, or being produced by a transporter-mediated process.

Unreactive A

In this example (Fig 2) n_A is kept constant, but the volume V increases with rate $\dot{V}$.

Fig 2. A is present inside the cell with a constant amount of n_A moles, while the cellular volume V increases with rate $\dot{V}$.

As V increases the concentration of A will decrease, i.e.,

$$\begin{array}{c}\hfill A=\frac{n_A}{V}\Rightarrow \dot{A}=\frac{\dot{n_A}}{V}+n_A·\frac{\left(\text{d}\frac{1}{V}\right)}{\text{d}t}=\frac{\dot{n_A}}{V}-n_A·\frac{\dot{V}}{V^2}=\frac{\dot{n_A}}{V}-A·\frac{\dot{V}}{V}\end{array}$$ (4)

Since we assume that n_A is constant, we have that $\dot{n_A}=0$ and the concentration of A decreases according to

$$\begin{array}{c}\hfill \dot{A}=-A·\frac{\dot{V}}{V}\Rightarrow \frac{\dot{A}}{A}=-\frac{\dot{V}}{V}\Rightarrow \frac{\text{d}log\left(A\right)}{\text{d}t}=-\frac{\text{d}log\left(V\right)}{\text{d}t}\end{array}$$ (5)

Integrating Eq 5 leads to:

$$\begin{array}{c}\hfill log\left(A\left(t\right)\right)-log\left(A_0\right)-\{logV\left(t\right)-log{V}_0\}\Rightarrow log\left(\frac{A\left(t\right)}{A_0}\right)=log\left(\frac{V_0}{V\left(t\right)}\right)\end{array}$$ (6)

which can be rewritten as

$$\begin{array}{c}\hfill A\left(t\right)=A_0\left(\frac{V_0}{V\left(t\right)}\right)\iff A\left(t\right)V\left(t\right)=A_0{V}_0\end{array}$$ (7)

Eq 7 can also be derived by noting that A₀ = n_A/V₀ and A(t) = n_A/V(t). Solving for n_A from one of the equations and inserting it into the other leads to Eq 7.

Cell internal generated A

In order to counteract diminishing levels of a controlled compound A compensatory fluxes can be generated by a cell internal compound (assumed here to be homogeneously distributed inside V) or by the help of transporters from stores outside of the cell or from cell-internal (organelle) stores. We will investigate both ways to generate compensatory fluxes.

To achieve a constant level of A from a cell internal source, despite increasing V, we consider first a zero-order enzymatic reaction where enzyme E converts a species S (assumed to be present in sufficiently high amounts) to A, where V is assumed to increase by a constant rate (Fig 3).

Fig 3. A is formed by zero-order kinetics within the cell while the cellular volume increases with a constant rate $\dot{V}=k_1$.

We assume that E is not subject to any synthesis, but that during the increase of V, E remains always saturated with S and produces A by zero-order kinetics with respect to A. The initial production rate of A at time t = 0 is given as

$$\begin{array}{c}\hfill {\dot{A}}_0=\frac{v_{max,0}·S_0}{K_M+S_0}\end{array}$$ (8)

Since E is considered to be saturated by S at all times we have that K_M ≪ S(t) leading to

$$\begin{array}{c}\hfill {\dot{A}}_0=v_{max,0}=k_2·E_0\end{array}$$ (9)

where k₂ is the turnover number of the enzymatic process generating A, and E₀ is the enzyme concentration at time t = 0. As volume V increases, the concentrations of E and A are subject to dilution as described by the rate equations

$$\begin{array}{c}\hfill \dot{E}=-E·\frac{\dot{V}}{V}\end{array}$$ (10)

$$\begin{array}{c}\hfill \dot{A}=k_2·E-A·\frac{\dot{V}}{V}\end{array}$$ (11)

For $\dot{V}$ = k₁ = constant, E(t) and A(t) are described by the equations (S1 Text)

$$\begin{array}{c}\hfill E\left(t\right)=E_0·\frac{\alpha }{t+\alpha };\alpha =\frac{V_0}{k_1}\end{array}$$ (12)

$$\begin{array}{c}\hfill A\left(t\right)=k_2·E_0·\alpha -(k_2·E_0·\alpha -A_0)·\frac{\alpha }{t+\alpha }\end{array}$$ (13)

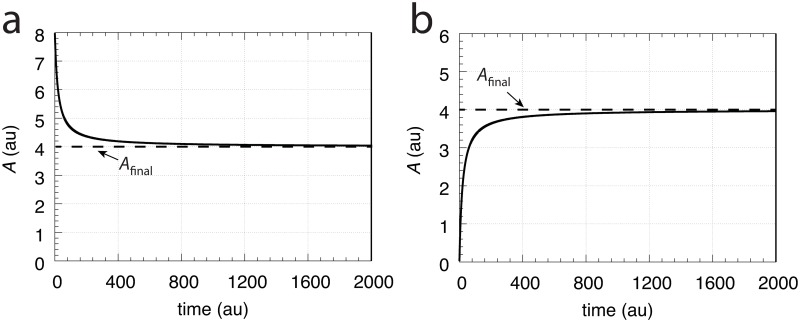
From Eq 13 we see that A will approach a final concentration A_final = k₂⋅E₀⋅α even when V continues to grow. The time needed of A to approach A_final is determined by the term α/(t+α).

Fig 4 shows that A_final is independent of the initial values of A. However, the system is not stable against perturbations which remove A. In such a case A will go to zero (S1 Text).

Fig 4. A approaches A_final independent of the initial concentration of A.

(a) A₀ = 8.0; (b) A₀ = 0.0. All other rate parameters are: $k_1=\dot{V}=1.0$, k₂ = 2.0, E₀ = 0.1, V₀ = 20.0.

Transporter generated A

Alternatively, A may be imported into the cell by a transporter T (Fig 5).

Fig 5. A is imported into the cell by transporter T.

Also here we consider that the transporter works under saturation (zero-order) conditions adding $\dot{n_A}$ moles of A per time unit into the cellular volume V

$$\begin{array}{c}\hfill \dot{n_A}=\frac{k_2·T·A_{ext}}{K_M^T+A_{ext}}\simeq k_2·T\end{array}$$ (14)

where T denotes the (surface/membrane) concentration of the transporter, $K_M^T$ is a dissociation constant between external A (A_ext) and T, and k₂ is the turnover number of the transporter-mediated uptake of A.

The change in the concentration of A inside an expanding cell is given by (see Eq 3)

$$\begin{array}{c}\hfill \dot{A}=\frac{\dot{n_A}}{V}-A\left(\frac{\dot{V}}{V}\right)=\frac{k_2·T}{V}-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (15)

For constant $\dot{V}$, k₂, and T the steady state of A ($\dot{A}=0$) is $k_{2}T/\dot{V}$ independent of the initial concentration of A. However, also in the transporter-based inflow of A, the steady state in A is not stable against perturbations removing A. Any reaction within the cell removing A while growth occurs will drive A to zero (S2 Text). To get a steady state that is stable against perturbations a negative feedback controller needs to be included.

Case A.1: Controllers with transporter-based compensatory fluxes and linear time-dependent perturbations

In this section the four controller motifs (Fig 1) are tested using a transporter-based compensatory flux with respect to constant growth, $\dot{V}=k_1$. In addition, an outflow perturbation with a time-dependent rate parameter k₃ is invoked, which removes A as a first-order reaction with respect to A.

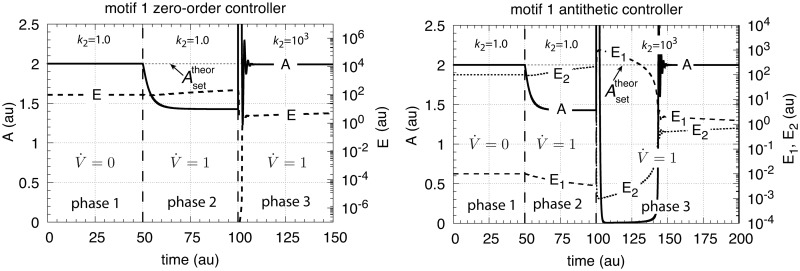
Motif 1 zero-order controller

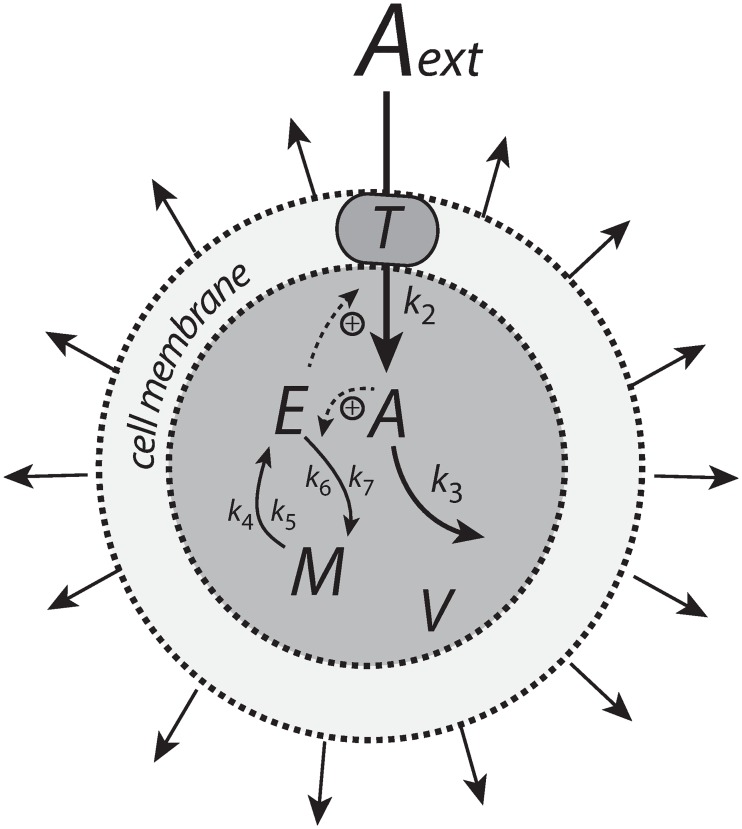
Fig 6 shows the motif 1 controller with zero-order implementation of integral control [7]. A is the controlled compound and E is the controller molecule which concentration (in the ideal controller case) is proportional to the integrated error between A and $A_{set}^{theor}$. M is considered as a store/precursor into which “consumed” E is recycled to. M is included to make it explicit that even under recycling conditions the increasing demand for E under growth and other time-dependent perturbations leads to a continuous reduction in M. This may lead to controller breakdown once all M is consumed. A situation when this occurs will be shown below for the motif 1 autocatalytic controller.

Fig 6. Motif 1 based zero-order integral controller with a transporter (T) generated compensatory flux.

The controller species E is produced by an enzymatic zero-order process from compound M. E is recycled by another zero-order process (with respect to E) but the rate of E-removal is proportional to the concentration of A. Outflow perturbations are represented by the rate r₃ = k₃⋅A, where k₃ is either constant or increases linearly with time.

The rate equations for this system are:

$$\begin{array}{c}\hfill \dot{A}=\frac{\dot{n_A}}{V}-k_3·A-A\left(\frac{\dot{V}}{V}\right)=\frac{k_2·E·T}{V}\left(\frac{A_{ext}}{K_M^T+A_{ext}}\right)-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (16)

$$\begin{array}{c}\hfill \dot{E}=\frac{k_4·M}{k_5+M}-\left(\frac{k_6·E}{k_7+E}\right)A-E\left(\frac{\dot{V}}{V}\right)\end{array}$$ (17)

$$\begin{array}{c}\hfill \dot{M}=-\frac{k_4·M}{k_5+M}+\left(\frac{k_6·E}{k_7+E}\right)A-M\left(\frac{\dot{V}}{V}\right)\end{array}$$ (18)

For simplicity, T and $A_{ext}/(K_M^T+A_{ext})$ are set to 1 leading to an inflow rate in A of k₂E/V. When $\dot{k_3}=\dot{V}=0$, the set-point of the controller is (Ref. [7], S3 Text)

$$\begin{array}{c}\hfill A_{set}^{theor}=\frac{k_4}{k_6}\end{array}$$ (19)

independent of the inflow rate constant k₂ and the time-dependent outflow perturbation parameter k₃.

When $\dot{V}$ = constant the zero-order controller maintains a steady state below $A_{set}^{theor}$ (S3 Text):

$$\begin{array}{c}\hfill A_{ss}=\frac{k_4}{k_6+\frac{2\dot{V}{k}_3}{k_2}}\end{array}$$ (20)

which is dependent of $\dot{V}$, and the rate constants k₂ and k₃.

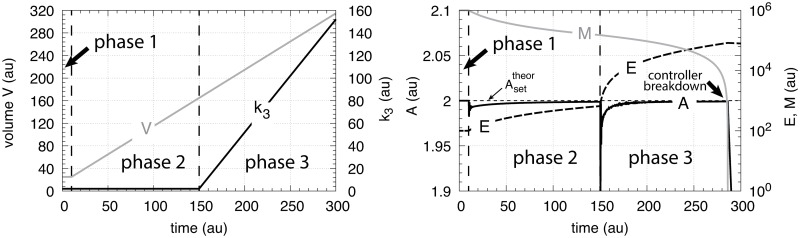
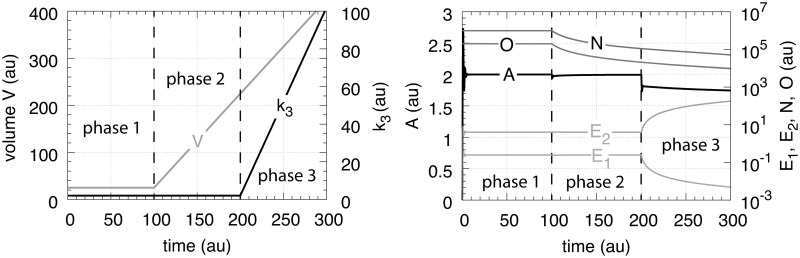
In testing the performance of this controller we consider three phases (see Fig 7). During the first phase the volume and the perturbation k₃ are kept constant. The controller is able to compensate for the perturbation rate k₃⋅A and keeps A at its theoretical set-point $A_{set}^{theor}$. In the second phase the volume increases linearly with time, while k₃ remains constant. The zero-order controller is now no longer able to maintain homeostasis at $A_{set}^{theor}=k_4/k_6$, but shows a $\dot{V}$-dependent offset below $A_{set}^{theor}$ as described by Eq 20. When k₃ increases linearly during phase 3 along the increase in V the controller breaks down and A goes to zero.

Fig 7. Performance of the motif 1 zero-order controller with transporter mediated compensatory flux (Eqs 16–18).

Phase 1: constant volume V and constant k₃. Initial concentrations and rate constant values: V₀ = 25.0, $\dot{V}=0.0$, A₀ = 0.0, E₀ = 0.0, M₀ = 4 × 10⁴, k₂ = 1.0, k₃ = 2.0, $\dot{k_3}=0.0$, k₄ = 20.0, k₅ = 1 × 10⁻⁶, k₆ = 10.0, k₇ = 1 × 10⁻⁶. The controller keeps A at its theoretical set-point, $A_{set}^{theor}=k_4/k_6=2.0$ (Eq 19). Phase 2: rate constants remain the same as in phase 1, but V increases linearly with $\dot{V}=2.0$, while k₃ remains constant at k₃ = 2.0. In agreement with Eq 20, the controller shows an offset below $A_{set}^{theor}$ with A_ss = 1.11. Phase 3: V continues to increase with the same speed while k₃ starts to increase linearly with $\dot{k_3}=1.0$. As indicated by Eq 20 the controller now breaks down and A goes to zero as V and k₃ increase.

Motif 1 antithetic controller

The antithetic controller [22] uses two controller molecules, E₁ and E₂ (Fig 8). Compound E₁ is activated by A but is removed by compound E₂ by a second-order process. E₂ is formed by a zero-order process which acts as a constant reference rate. In addition, E₂ also acts as a signaling molecule, which closes the negative feedback loop by activating the transporter-based compensatory inflow of A.

Fig 8. Motif 1 based controller with second-order (antithetic) integral control.

The controller species E₂ is produced by an enzymatic zero-order process from compound O. E₂ activates the transporter-based compensatory flux of A and is removed by E₁ using second-order kinetics forming P.

Assuming, as in the previous two examples that T and $A_{ext}/(K_M^T+A_{ext})$ are both 1, the rate equations are

$$\begin{array}{c}\hfill \dot{A}=\frac{\dot{n_A}}{V}-k_3·A-A·\frac{\dot{V}}{V}=\frac{k_2·E_2}{V}-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (21)

$$\begin{array}{c}\hfill \dot{E_1}=A\left(\frac{k_4·M}{k_5+M}\right)-k_6·E_1·E_2-E_1\left(\frac{\dot{V}}{V}\right)\end{array}$$ (22)

$$\begin{array}{c}\hfill \dot{E_2}=\frac{k_8·O}{k_9+O}-k_6·E_1·E_2-E_2\left(\frac{\dot{V}}{V}\right)\end{array}$$ (23)

$$\begin{array}{c}\hfill \dot{M}=-A\left(\frac{k_4·M}{k_5+M}\right)-M\left(\frac{\dot{V}}{V}\right)\end{array}$$ (24)

$$\begin{array}{c}\hfill \dot{O}=-\frac{k_8·O}{k_9+O}-O\left(\frac{\dot{V}}{V}\right)\end{array}$$ (25)

$$\begin{array}{c}\hfill \dot{Q}=k_3·A-Q\left(\frac{\dot{V}}{V}\right)\end{array}$$ (26)

$$\begin{array}{c}\hfill \dot{P}=k_6·E_1·E_2-P\left(\frac{\dot{V}}{V}\right)\end{array}$$ (27)

where k₅ ≪ M and k₉ ≪ O such that the generation of E₁ and E₂ are zero-order processes with respect to M and O.

In case $\dot{V}=0$ and $\dot{k_3}=0$ the set-point of the controller is given by setting Eqs 22 and 23 to zero. Eliminating the second-order term k₆⋅E₁⋅E₂ leads to

$$\begin{array}{c}\hfill A_{set}^{theor}=\frac{k_8}{k_4}=2.0\end{array}$$ (28)

which is shown in phase 1 of Fig 9. In phase 2 the volume increases linearly with $\dot{V}=2.0$ (Fig 9, left panel) while k₃ remains to be constant at k₃ = 2.0. The controller is no longer able to keep A at its theoretical set-point (Eq 28). When $\dot{V}$ and k₃ are constant an analytical expression of A_ss can be derived in good agreement with the numerical calculations (S4 Text):

$$\begin{array}{c}\hfill A_{ss}=\frac{k_2{k}_8}{k_2{k}_4+2k_3\dot{V}}\end{array}$$ (29)

which is analogous to the A_ss expression of the motif 1 zero-order controller (Eq 20). Finally, in phase 3 k₃ increases linearly with $\dot{k_3}=1$ together with $\dot{V}=2.0$. As indicated by Eq 29 and shown by the numerical calculations (Fig 9) the antithetic controller, like the zero-order controller, breaks down and A goes to zero (S4 Text).

Fig 9. Performance of the antithetic controller with transporter mediated compensatory flux (Eqs 21–27).

Phase 1: constant volume V and constant k₃. Initial concentrations and rate constant values: V₀ = 25.0, $\dot{V}=0.0$, A₀ = 0.0, E_1,0 = 0.0, E_2,0 = 0.0, M₀ = 1 × 10⁵, O₀ = 1 × 10⁵, k₂ = 1.0, k₃ = 2.0, $\dot{k_3}=0.0$, k₄ = 10.0, k₅ = 1 × 10⁻⁶, k₆ = 20.0, k₇ not used, k₈ = 20.0, k₉ = 1 × 10⁻⁶. The controller keeps A at its theoretical set-point at $A_{set}^{theor}=k_8/k_4=2.0$ (Eq 28). Phase 2: rate constants remain the same as in phase 1, but V increases linearly with $\dot{V}=2.0$, while k₃ remains constant at k₃ = 2.0. The controller shows an offset below $A_{set}^{theor}$ with A_ss = 1.11 in agreement with Eq 29. Phase 3: V continues to increase while k₃ increases linearly with $\dot{k_3}=1.0$. As indicated by Eq 29 the controller breaks down and A goes to zero.

Although not shown explicitly here, the following mass balances are obeyed:

$$\begin{array}{c}\hfill n_{M,0}=n_M\left(t\right)+n_{E_1}\left(t\right)+n_P\left(t\right)\end{array}$$ (30)

$$\begin{array}{c}\hfill n_{O,0}=n_O\left(t\right)+n_{E_2}\left(t\right)+n_P\left(t\right)\end{array}$$ (31)

where n_i,0 and n_i are respectively the initial number of moles and the number of moles at time t of compound i.

As described above, when using a transporter mediated compensation in A the antithetic and the motif 1 zero-order controllers have to increase their controller variables E₂ or E in order to keep A_ss constant, as indicated by the equation

$$\begin{array}{c}\hfill \dot{A}=0\Rightarrow \frac{k_2·E_{\left(2\right)}\left(t\right)}{V\left(t\right)}=k_3·A_{ss}\end{array}$$ (32)

where E₍₂₎ represents E₂ or E and $(\dot{V}/V)A_{ss}$ becomes negligible.

Motif 1 autocatalytic controller

Similar to controllers based on double integral action [24] an autocatalytic design [19] is able to keep the controlled species at its set-point even when perturbations become linearly time dependent and rapid [18]. However, in contrast to double integral action the autocatalytic controller is able to compensate for time-dependent perturbations of the form a⋅tⁿ where n is larger than 1.

Fig 10 shows the reaction scheme. The controller compound E is produced autocatalytically, i.e., its rate is proportionally to the concentration of E, while M, present in relative large amounts, produces E by an enzyme-catalyzed reaction which is zero-order with respect to M. E increases the activity of transporter T and leads to an increased import of external A into the cell. The negative feedback is closed by an A-induced recycling of E to M. Rate constant k₃ represents a perturbation which removes A by a first-order process with respect to A. The rate equations are:

$$\begin{array}{c}\hfill \dot{A}=\frac{\dot{n_A}}{V}-k_3·A-A\left(\frac{\dot{V}}{V}\right)=\frac{k_2·E·T}{V}\left(\frac{A_{ext}}{K_M^T+A_{ext}}\right)-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (33)

$$\begin{array}{c}\hfill \dot{E}=E\left(\frac{k_4·M}{k_5+M}\right)-k_6·E·A-E\left(\frac{\dot{V}}{V}\right)+k_E^{in}-k_E^{out}·E\end{array}$$ (34)

$$\begin{array}{c}\hfill \dot{M}=-E\left(\frac{k_4·M}{k_5+M}\right)+k_6·E·A-M\left(\frac{\dot{V}}{V}\right)\end{array}$$ (35)

Fig 10. Motif 1 autocatalytic integral controller.

The controller species E is produced by an enzymatic zero-order process from compound M, but E activates its own production and the transporter-based compensatory flux. The negative feedback is due to the inflow activation of A by E through transporter T, while A activates the (first-order) recycling of E to M. Outflow perturbation in A is described by the rate k₃⋅A, where k₃ is either a constant or increases linearly with time. $k_E^{in}$ and $k_E^{out}$ represent background reactions creating and removing E.

As in the previous cases, in Eq 33, the term $T·A_{ext}/(K_M^T+A_{ext})$ is set to 1. The last two terms in Eq 34, $k_E^{in}-k_E^{out}·E$, represent required background reactions to keep E at a sufficiently high level such that the autocatalysis in E can start at low/zero initial E concentrations (see also Ref. [18] and Discussion there). In the calculations presented here, $k_E^{in}$ and $k_E^{out}$ are set to 1×10⁻⁵. To show that in this case the controller can start from initial concentration E₀ = 0, see the corresponding calculation later in the paper when using a cell-internal compensatory flux, or test it using S1 Matlab for Fig 11. When E₀ is larger than 10⁻⁵ the $k_E^{in}-k_E^{out}·E$ term is not needed, but its presence will not affect controller dynamics or set-point as long as $k_E^{in}$ and $k_E^{out}$ are kept low. In case the $k_E^{in}$ and $k_E^{out}$ values are higher, a change/reduction in the set-point is observed, which the controller still defends (see later in this chapter).

Fig 11. Performance of the motif 1 autocatalytic controller (Eqs 33–35).

Phase 1: constant volume V and constant k₃. Initial concentrations and rate constant values (at the controller’s steady state): V₀ = 25.0, $\dot{V}=0.0$, A₀ = 2.0, E₀ = 100.0, M₀ = 1 × 10⁶, k₂ = 1.0, k₃ = 2.0, $\dot{k_3}=0.0$, k₄ = 20.0, k₅ = 1 × 10⁻⁶, k₆ = 10.0, $k_E^{in}=k_E^{out}=1\times {10}^{-5}$. The controller keeps A at its set-point at $A_{set}^{theor}=k_4/k_6=2.0$. Phase 2: rate constants remain the same as in phase 1, but V increases linearly with $\dot{V}=1.0$. Phase 3: V continues to increase with the same rate and k₃ increases with rate $\dot{k_3}=1.0$. The controller moves A towards $A_{set}^{theor}$ in both phase 2 and phase 3, but breaks down when no additional E becomes available through M (indicated by the arrow in the right panel).

To determine the controller’s set-point at constant V and k₃ we set Eq 34 to zero. Neglecting the $k_E^{in}-k_E^{out}·E$ term and setting $\dot{V}=0$, we can solve for the steady state value of A, which defines the controller’s theoretical set-point $A_{set}^{theor}$:

$$\begin{array}{c}\hfill \dot{E}=E_{ss}\left(\frac{k_4·M}{k_5+M}\right)-k_6·E_{ss}·A_{ss}=E_{ss}\left[\right(\frac{k_4·M}{k_5+M})-k_6·A_{ss}]=0\end{array}$$ (36)

Since M/(k₅ + M) = 1 (ideal zero-order conditions), we get from Eq 36

$$\begin{array}{c}\hfill k_4-k_6·A_{ss}=0\Rightarrow A_{ss}=A_{set}^{theor}=\frac{k_4}{k_6}\end{array}$$ (37)

For constant $\dot{V}$ and $\dot{k_3}$ values the set-point is calculated to be (S5 Text)

$$\begin{array}{c}\hfill A_{ss}=\frac{k_4}{k_6}-\frac{\dot{k_3}}{k_6·k_3}\to \frac{k_4}{k_6}=A_{set}^{theor}\text{as}t\to \infty \end{array}$$ (38)

According to previous findings on the autocatalytic controller [18], any time-dependent function k₃(t) = k_3,0 + a⋅tⁿ where a, n > 0 will lead to the set-point conditions described by Eq 38 (S5 Text).

The recycling scheme between E and M implies that E and M obey a mass balance of the form

$$\begin{array}{c}\hfill n_E\left(t\right)+n_M\left(t\right)=n_{E,0}+n_{M,0}\end{array}$$ (39)

with n_E(t) = E(t)⋅V(t), n_M(t) = M(t)⋅V(t), and where n_E,0 and n_M,0 are the initial number of moles of respectively E and M. The rates how n_E and n_M change at a given time t are given as (S5 Text)

$$\begin{array}{c}\hfill \dot{n_E}=[\dot{E}+E(\frac{\dot{V}}{V}\left)\right]·V=-\dot{n_M}=-[\dot{M}+M(\frac{\dot{V}}{V}\left)\right]·V\end{array}$$ (40)

Fig 11 shows the results. During the first phase no volume change occurs and k₃ is a constant. The controller keeps A at $A_{set}^{theor}=2.0$ as described by Eq 37. During the second phase both V and k₃ increase linearly and the controller still keeps A at $A_{set}^{theor}=2.0$ according to Eq 38. To keep A at its set-point during increasing V and/or k₃ the concentration of E has to increase in order to maintain the steady state condition given by Eq 33 when $\dot{A}=0$ and $\dot{V}/V\to 0$, i.e.,

$$\begin{array}{c}\hfill E\left(t\right)=\frac{k_3\left(t\right)·V\left(t\right)·A_{ss}}{k_2}\end{array}$$ (41)

From the initial conditions (see legend of Fig 11) we have that n_E(t) + n_M(t) = V₀ ⋅ M₀ = 2.5 × 10⁷.

When $k_E^{in}$ and $k_E^{out}$ are significantly higher than 10⁻⁵, then the set-point of the controller changes to the following steady state value in A:

$$\begin{array}{c}\hfill A_{ss}\approx \frac{k_4-k_E^{out}}{k_6}\end{array}$$ (42)

The new set-point is defended by the controller for step-wise changes and for linearly increasing values of k₃ and V (for details, see S5 Text).

Motif 2 zero-order controller

The reaction scheme of this controller is shown in Fig 12. The transporter-based compensatory flux is regulated by E through repression or derepression by E. E is removed by a zero-order reaction creating M, which then is recycled in a A-dependent manner.

Fig 12. Motif 2 based controller with zero-order integral control.

An increase of the compensatory flux occurs by a decrease of E (derepression of the compensatory flux).

The rate equations are

$$\begin{array}{c}\hfill \dot{A}=\frac{\dot{n_A}}{V}-k_3·A-A\left(\frac{\dot{V}}{V}\right)=\frac{k_2{k}_4}{k_4+E}\left(\frac{T·A_{ext}}{K_M^T+A_{ext}}\right)·\frac{1}{V}-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (43)

$$\begin{array}{c}\hfill \dot{E}=\left(\frac{k_8·M}{k_{11}+M}\right)·A-\frac{k_9·E}{k_{10}+E}-E\left(\frac{\dot{V}}{V}\right)\end{array}$$ (44)

$$\begin{array}{c}\hfill \dot{M}=-\left(\frac{k_8·M}{k_{11}+M}\right)·A+\frac{k_9·E}{k_{10}+E}-M\left(\frac{\dot{V}}{V}\right)\end{array}$$ (45)

$$\begin{array}{c}\hfill \dot{P}=k_3·A-P\left(\frac{\dot{V}}{V}\right)\end{array}$$ (46)

Also here, we keep for the sake of simplicity, $T·A_{ext}/(K_M^T+A_{ext})=1$. In presence of growing V and k₃ the motif 2 zero-order controller successfully defends its theoretical set-point given by (S6 Text)

$$\begin{array}{c}\hfill A_{set}^{theor}=\frac{k_9}{k_8}\end{array}$$ (47)

However, since an increase of the compensatory flux is based on derepression by E (decreasing E), the controller will break down when E ≪ k₄ or k₄/(k₄+E)≈1. Neglecting the $A·\dot{V}/V$ term, the point when the breakdown occurs can be estimated by setting Eq 43 to zero

$$\begin{array}{c}\hfill \dot{A}=\frac{k_2}{V}-k_3·A_{set}^{theor}=0\Rightarrow k_3·V=\frac{k_2}{A_{set}^{theor}}\end{array}$$ (48)

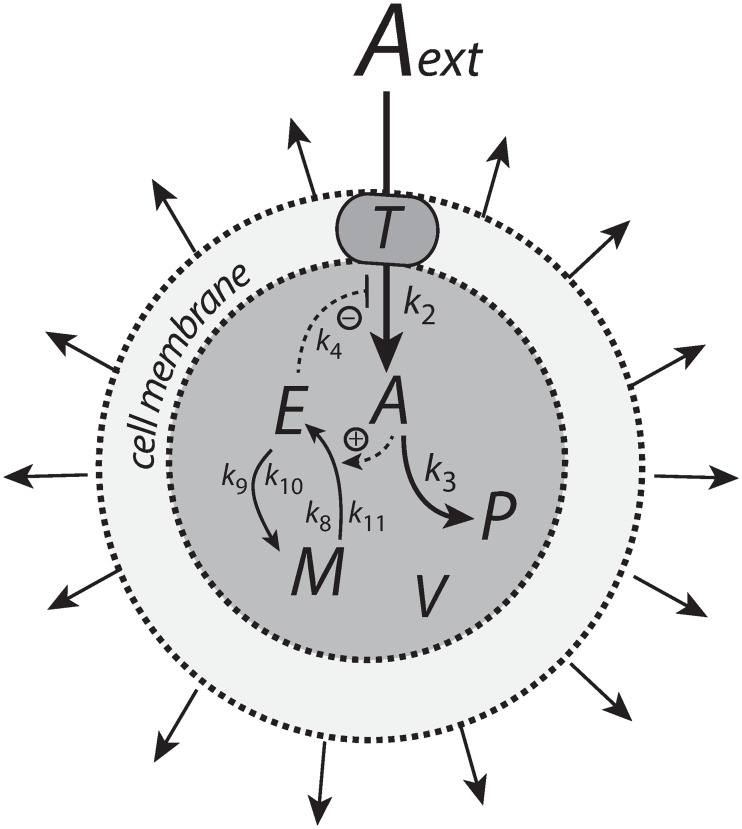
Fig 13 shows that the motif 2 based controller is able to defend successfully against linear growth in both V and k₃ and keeping A at $A_{set}^{theor}$. Prolonged time intervals with increasing V and k₃ will lead to controller breakdown when the condition of Eq 48 is met. The condition k₄/(k₄+E)≈1 also indicates that the capacity limit of the controller has been reached, because the compensatory flux k₂ k₄/(k₄+E) (Eq 43) has reached its maximum value k₂ and can no longer be increased.

Fig 13. Performance of the motif 2 zero-order based controller with respect to linear increases in V and k₃.

The controller is able to defend $A_{set}^{theor}$ successfully, but breaks down when k₃V reaches $k_2/A_{set}^{theor}$ (Eq 48). Rate parameters: k₂ = 1 × 10⁵, k₄ = 1 × 10⁻³, k₈ = 1.0, k₉ = 2.0, k₁₀ = k₁₁ = 1 × 10⁻⁶. Initial conditions: $A_0=A_{set}^{theor}=2.0$, E₀ = 1.0, M₀ = 1 × 10⁶, P₀ = 0.0, V₀ = 25.0, k_3,0 = 2.0. $\dot{V}=2.0$ (phase 2 and phase 3), $\dot{k_3}=1.0$ (phase 3).

Case A.2: Controllers with transporter-based compensatory fluxes and exponential time-dependent perturbations

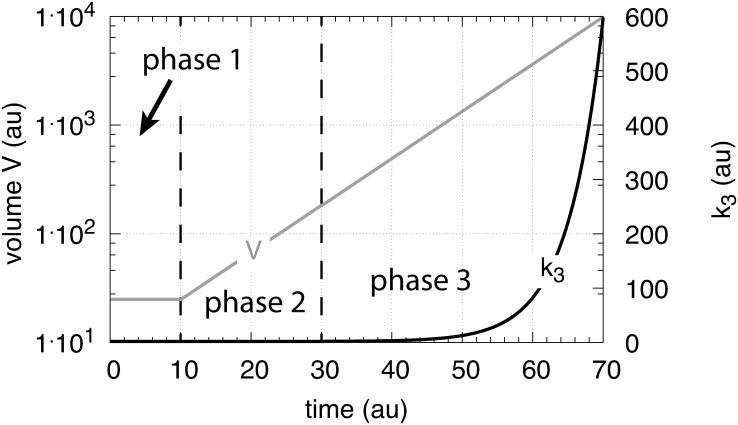
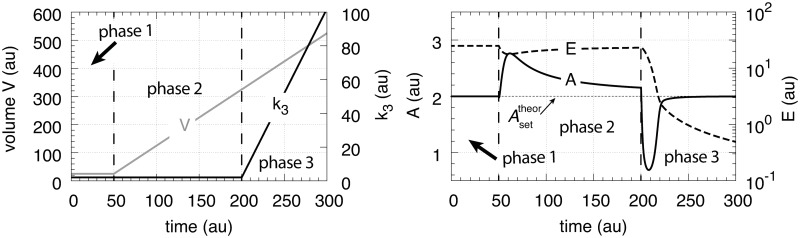
Here we describe the performance of the four controller motifs (Fig 1) with transporter-based compensatory fluxes when exposed to exponential growth, $\dot{V}=\kappa ·V$, and an exponential increase in the outflow perturbation rate parameter k₃ (Fig 14).

Fig 14. The perturbation profile with exponential growth of V and k₃.

Due to presentation reasons V is plotted semi-logarithmically while the k₃ scale is linear.

There are three phases the controllers are exposed to. During the first phase the controllers are at their steady states and V and k₃ are kept constant at respectively 25.0 and 2.0. During the second phase V increases exponentially according to $\dot{V}=\kappa V$ (κ = 0.1), while k₃ is kept constant at 2.0. During phase 3, V continues to grow exponentially and k₃ starts to increase according to

$$\begin{array}{c}\hfill k_3\left(t\right)=k_{3,p3}+0.2({\text{e}}^{0.2(t-t_{p3})}-1)\end{array}$$ (49)

where k_3,p3 and t_p3 are the values of respectively k₃ and time t at the beginning of phase 3.

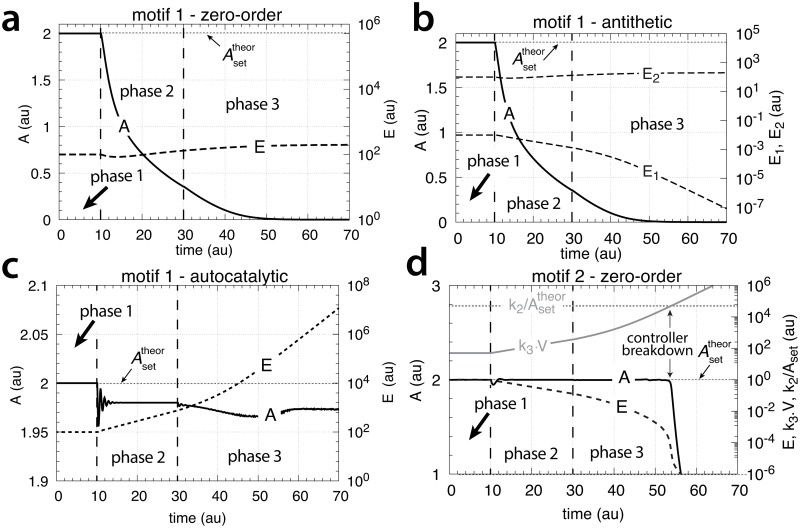
Fig 15 shows that only the motif 2 based controller with derepression kinetics (panel d) is able to counteract both exponential increases in V and k₃. However, due to the derepression kinetics and due to the transporter based kinetics (see Eq 48) the controller breaks down when the product of the perturbations, k₃V reaches $k_6/A_{set}^{theor}$. The motif 1 autocatalytic controller (panel c) shows slight constant offsets below $A_{set}^{theor}$, as expected [18], both for the single exponential increase of V during phase 2 and when both V and k₃ increase exponentially in phase 3. These offsets increase when the values of $k_E^{in}$ and $k_E^{out}$ are large and cannot be neglected (S5 Text). Since E increases with increasing perturbation strengths the controller is limited by the supply for E via M as indicated in Fig 11. Neither the motif 1 based zero-order controller (panel a) nor the antithetic controller based on motif 1 (panel b) are able to compensate for exponentially increasing perturbation strengths. They behave very similar, as already seen in Figs 7 and 9 for linear time-dependent perturbations.

Fig 15. Performance of the (a) motif 1-zero-order, (b) -antithetic, (c) -autocatalytic, and (d) motif 2 zero-order controllers with transporter-based compensatory fluxes in relation to the perturbation profile of Fig 14.

For rate equations of the individual controllers, see the descriptions in the previous sections dealing with linear time-dependent perturbations. Rate parameters and initial conditions: (a) see legend of Fig 7, (b) see Fig 9, (c) see Fig 11, but using M₀ = 1×10¹⁰, and (d) see Fig 13.

Growth related to surface to volume ratio and controllers with transporter-based compensatory fluxes

We have investigated how the controllers with transporter-based compensatory fluxes behave with respect to the growth law described by Eq 2 (η = 1 and ξ = 0.2) when k₃ increases exponentially in phase 3 according to Eq 49 (Fig 16a).

Fig 16. Performance of the motif 1 antithetic, motif 1 autocatalytic and motif 2 zero-order controllers with respect to surface to volume ratio related growth and an exponential increase of k₃.

(a) Perturbation profile. Phase 1: constant V (25.0) and k₃ (2.0); phase 2: V increases according to Eq 2 (η = 1 and ξ = 0.2) and k₃ remains constant; phase 3: V continues to increase and k₃ starts to increase exponentially as described by Eq 49. (b) Behavior of the antithetic controller (Eqs 21–27). Rate constant values as in Fig 9. Initial concentrations: A₀ = 2.0, E_1,0 = 0.01, E_2,0 = 100, M₀ = O₀ = 1 × 10⁶. (c) Behavior of the autocatalytic controller (Eqs 33–35). Rate constant values as in Fig 11. Initial concentrations: A₀ = 2.0, E₀ = 0.01, M₀ = 1 × 10⁶. (d) Behavior of the motif 2 zero-order controller (Eqs 43–46). Initial concentrations: A₀ = 2.0, E₀ = 1.0, M₀ = 1 × 10³. Note the breakdown of the controller at the very end of phase 3 due to low E (arrow).

Fig 16b–16d show the results of the antithetic, motif 1 autocatalytic and motif 2 zero-order controllers. The motif 1 zero-order controller’s behavior of A is identical to that of the antithetic controller and only the result of the antithetic controller is shown. Typically for this type of growth law is that the motif 1 based controllers gain successively control during phase 2 when $\dot{V}$ decreases and approaches zero. During phase 3, when k₃ increases exponentially, only the motif 2 based is able to defend its theoretical set-point, but breaks down when E become too low. The autocatalytic controller shows a constant offset below $A_{set}^{theor}$. Both the antithetic and the motif 1 zero-order controllers break down during phase 3 and A goes to zero.

Case B.1: Controllers with cell-internal compensatory fluxes and linear time-dependent perturbations

We consider here the four controllers, but the compensatory fluxes are now generated from cell-internal and homogeneously distributed sources.

Motif 1 zero-order controller

Fig 17 shows the motif 1 zero-order controller using a cell-internal compensatory flux. The homogenously distributed compound N serves as a source for A, which is activated by E. Compound M serves as a source for E, while by the activation of A, M is recycled from E.

Fig 17. Motif 1 zero-order controller with a cell-internal compensatory flux.

The rate equations are

$$\begin{array}{c}\hfill \dot{A}=k_2·E\left(\frac{N}{k_7+N}\right)-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (50)

$$\begin{array}{c}\hfill \dot{E}=\frac{k_4·M}{k_5+M}-\left(\frac{k_6·E}{k_8+E}\right)A-E\left(\frac{\dot{V}}{V}\right)\end{array}$$ (51)

$$\begin{array}{c}\hfill \dot{M}=-\frac{k_4·M}{k_5+M}+\left(\frac{k_6·E}{k_8+E}\right)A-M\left(\frac{\dot{V}}{V}\right)\end{array}$$ (52)

$$\begin{array}{c}\hfill \dot{N}=-\left(\frac{k_2·N}{k_7+N}\right)E-N\left(\frac{\dot{V}}{V}\right)\end{array}$$ (53)

$$\begin{array}{c}\hfill \dot{P}=-k_3·A-P\left(\frac{\dot{V}}{V}\right)\end{array}$$ (54)

The steady state of A when both $\dot{V}$ and $\dot{k_3}$ are constant is given by the following expression (S3 Text)

$$\begin{array}{c}\hfill A_{ss}=\frac{k_2{k}_4}{k_2{k}_6+\dot{k_3}}\end{array}$$ (55)

When $\dot{k_3}=0$ and $\dot{V}$ = constant A_ss becomes $A_{set}^{theor}=k_4/k_6$ and the motif 1 zero-order controller is able to compensate for a constant growth rate (Fig 18, phases 1 and 2). However, when k₃ increases linearly, A_ss is below $A_{set}^{theor}$ and remains constant as long as sufficient M and N are present (Fig 18, phase 3). Thus, in comparison with a transporter-mediated compensatory fluxes, the motif 1 zero-order controller with an internally generated compensatory flux shows an improved performance by being able to compensate for a constant growth rate in the absence of other outflow perturbations in A.

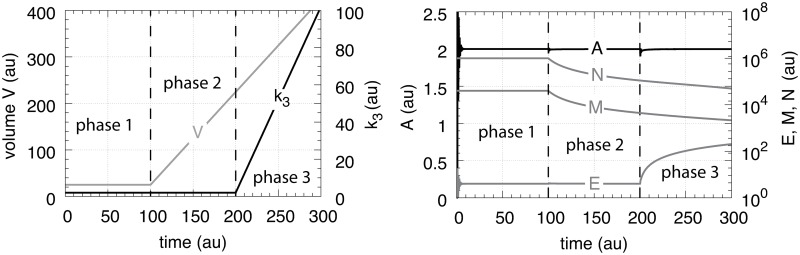
Fig 18. Performance of the motif 1 zero-order controller with internally generated compensatory flux (Fig 17; Eqs 50–54).

Phase 1: constant volume V and constant k₃. Initial volume, concentrations, and rate constants: V₀ = 25.0, $\dot{V}=0.0$, A₀ = 0.0, E₀ = 0.0, M₀ = 4 × 10⁴, N₀ = 1 × 10⁵, P₀ = 0.0, k₂ = 1.0, k₃ = 2.0, $\dot{k_3}=0.0$, k₄ = 20.0, k₅ = 1 × 10⁻⁶, k₆ = 10.0, k₇ = 1 × 10⁻⁶, k₈ = 1 × 10⁻⁶. The controller moves A to its set-point at $A_{set}^{theor}=(k_4/k_6)=2.0$ (Eq 55). Phase 2: rate constants remain the same as in phase 1, but V increases linearly with $\dot{V}=2.0$, while k₃ remains constant at k₃ = 2.0. The controller is able to keep A at $A_{set}^{theor}=(k_4/k_6)=2.0$ in agreement with Eq 55. Phase 3: V continues to increase with the same speed while k₃ now linearly increases with $\dot{k_3}=1.0$. As indicated by Eq 55 A_ss leads to a constant offset below $A_{set}^{theor}$.

Motif 1 antithetic controller

When the antithetic integral controller is equipped with an internally generated compensatory flux (Fig 19) its performance towards constant growth and linearly increasing outflow perturbations k₃ is significantly improved in comparison with a controller having a transporter generated compensatory flux (Fig 9). The rate equation for A is now changed to

$$\begin{array}{c}\hfill \dot{A}=\left(\frac{k_2·N}{k_7+N}\right)E_2-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (56)

while the other rate equations (Eqs 22–27) remain the same.

Fig 19. The antithetic controller with an internal generated compensatory flux.

When $\dot{V}$ is constant A_ss becomes (S4 Text)

$$\begin{array}{c}\hfill A_{ss}=\frac{k_2{k}_8}{k_2{k}_4+\dot{k_3}}\end{array}$$ (57)

As indicated by Eq 57 numerical results show (Fig 20, phase 2) that the antithetic controller is now able to compensate for linear volume increases by moving A to $A_{set}^{theor}=(k_8/k_4)$. However, an offset in A_ss below $A_{set}^{theor}$ is observed when, in addition, k₃ increases linearly with time, i.e., when $\dot{k_3}$ is constant.

Fig 20. Performance of the antithetic controller when the compensatory flux is homogeneously generated within the cellular volume (Eqs 56 and 22–27).

Phase 1: constant volume V and constant k₃. Initial concentrations and rate constant values: V₀ = 25.0, $\dot{V}=0.0$, A₀ = 0.0, E_1,0 = 0.0, E_2,0 = 0.0, M₀ = 2 × 10⁵, N₀ = 1 × 10⁶, O₀ = 2 × 10⁵, k₂ = 1.0, k₃ = 2.0, $\dot{k_3}=0.0$, k₄ = 10.0, k₅ = 1 × 10⁻⁶, k₆ = 20.0, k₇ = 1 × 10⁻⁵, k₈ = 20.0, k₉ = 1 × 10⁻⁵. The controller moves A to $A_{set}^{theor}=(k_8/k_4)=2.0$ (Eq 57 when $\dot{k_3}=0$). Phase 2: rate constants remain the same as in phase 1, but V increases linearly with $\dot{V}=2.0$, while k₃ remains constant at k₃ = 2.0. The controller is able to maintain A at $A_{set}^{theor}=k_4/k_6=2.0$ in agreement with Eq 57. Phase 3: V continues to increase with the same speed while k₃ now linearly increases with $\dot{k_3}=1.0$. As indicated by Eq 57 the controller is no longer able to keep A at $A_{set}^{theor}$ but shows a constant steady state value below its theoretical set-point.

Although not explicitly shown here, during the volume increase, the mass (mole) balances described by Eqs 30 and 31 are obeyed in addition to the mass balance connecting N, A, and Q

$$\begin{array}{c}\hfill n_{N,0}=n_N\left(t\right)+n_A\left(t\right)+n_Q\left(t\right)\end{array}$$ (58)

where n_N,0 is the number of moles of initial N at t = 0 with n_A,0 = n_Q,0 = 0.

Motif 1 autocatalytic controller

Fig 21 shows the autocatalytic controller but now with an internally generated compensatory flux. As for the motif 1 zero-order controller (Fig 17) the compensatory flux originates from compound N and is activated by E. N is present in high concentration and forms A by a zero-order process with respect to N.

Fig 21. Scheme of autocatalytic controller with an internally generated compensatory flux from compound N.

Otherwise the controller has the same structure as shown in Fig 10.

The rate equation for the controlled variable A is

$$\begin{array}{c}\hfill \dot{A}=k_2·E\left(\frac{N}{k_7+N}\right)-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (59)

while the rate equations for E and M remain the same as Eqs 34 and 35. Species P is included with the rate equation

$$\begin{array}{c}\hfill \dot{P}=k_3·A-P\left(\frac{\dot{V}}{V}\right)\end{array}$$ (60)

to test that the mass (mole) balance between N, A, and P is preserved.

The controller’s steady state in A is also in this case described by Eq 38 (S5 Text). In contrast to the other controllers, even when $\dot{V}$ and $\dot{k_3}$ are constant, the autocatalytic controller is able to move A to $A_{set}^{theor}=(k_4/k_6)$ (Fig 22).

Fig 22. Performance of the autocatalytic controller when the compensatory flux is generated within the cellular volume (Eqs 34, 35, 59 and 60).

Phase 1: constant volume V and constant k₃. Initial concentrations and rate constant values: V₀ = 25.0, $\dot{V}=0.0$, A₀ = 0.0, E₀ = 0.0, M₀ = 4 × 10⁴, N₀ = 1 × 10⁶, k₂ = 1.0, k₃ = 2.0, $\dot{k_3}=0.0$, k₄ = 20.0, k₅ = 1 × 10⁻⁶, k₆ = 10.0, k₇ = 1 × 10⁻⁶, $k_E^{in}=k_E^{out}=1\times {10}^{-5}$. The controller moves A to its theoretical set-point at $A_{set}^{theor}=(k_4/k_6)=2.0$ (Eq 37). Phase 2: rate constants remain the same as in phase 1, but V increases linearly with $\dot{V}=2.0$, while k₃ remains constant at k₃ = 2.0. The controller is able to maintain A at $A_{set}^{theor}$ in agreement with Eq 37. Phase 3: V continues to increase with the same speed while k₃ now linearly increases with $\dot{k_3}=1.0$. As indicated by Eq 38 the controller keeps A at $A_{set}^{theor}$ as k₃ increases.

When $k_E^{in}$ and $k_E^{out}$ are large and cannot be neglected the steady state in A is described by the quadratic equation (S5 Text)

$$\begin{array}{c}\hfill A_{ss}^2-A_{ss}(\frac{k_4-k_E^{out}}{k_6}-\frac{\dot{k_3}}{k_3{k}_6})-\frac{k_2{k}_E^{in}}{k_3{k}_6}=0\end{array}$$ (61)

In case only V increases linearly A_ss is given by the solution of Eq 61, independent of V’s growth rate. On the other hand, if k₃ increases linearly, the terms $\dot{k_3}/k_3{k}_6$ and $k_2{k}_E^{in}/k_3{k}_5$ go to zero for large k₃ and A_ss is given by $(k_4-k_E^{out})/k_6$ as described by Eq 42 for the transporter-based compensatory flux.

Motif 2 zero-order controller

The rate equations for the motif 2 controller using a cell-internal compensatory flux are (Fig 23):

$$\begin{array}{c}\hfill \dot{A}=\left(\frac{k_4·k_6}{k_4+E}\right)·\left(\frac{N}{k_7+N}\right)-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (62)

$$\begin{array}{c}\hfill \dot{E}=\left(\frac{k_8·M}{k_{11}+M}\right)·A-\frac{k_9·E}{k_{10}+E}-E\left(\frac{\dot{V}}{V}\right)\end{array}$$ (63)

$$\begin{array}{c}\hfill \dot{M}=-\left(\frac{k_8·M}{k_{11}+M}\right)·A+\frac{k_9·E}{k_{10}+E}-M\left(\frac{\dot{V}}{V}\right)\end{array}$$ (64)

$$\begin{array}{c}\hfill \dot{N}=-\left(\frac{k_4·k_6}{k_4+E}\right)·\left(\frac{N}{k_7+N}\right)-N\left(\frac{\dot{V}}{V}\right)\end{array}$$ (65)

$$\begin{array}{c}\hfill \dot{P}=k_3·A-P\left(\frac{\dot{V}}{V}\right)\end{array}$$ (66)

Fig 24 shows the performance of the motif 2 feedback structure with zero-order integral control. The controller is able to defend successfully $A_{set}^{theor}$ against a linear increase in V (phase 2) as well as against linear increase in V and a simultaneous linear increase in k₃ (phase 3). For both cases the controller will move A precisely to $A_{set}^{theor}=k_9/k_8$ without any offset (see S6 Text for details).

Fig 23. Motif 2 type controller with integral control based on zero-order kinetics and a cell-internally generated compensatory flux from compound N.

Fig 24. Performance of the motif 2 feedback scheme with zero-order based integral control and a cell-internal compensatory flux.

Rate constants and initial conditions: k₃ = 2.0, k₄ = 1 × 10⁻³, k₆ = 1 × 10⁵, k₇ = 1 × 10⁻⁶, k₈ = 1.0, k₉ = 2.0, k₁₀ = k₁₁ = 1 × 10⁻⁶, A₀ = 2.0, E₀ = V₀ = 25.0, M₀ = 1 × 10⁶, N₀ = 3 × 10⁶. Phase 1: V and k₃ remain unchanged. Phase 2: V increases linearly with $\dot{V}=2.0$, while k₃ remains constant. Phase 3: V continues to increase and k₃ increases linearly with $\dot{k_3}=1.0$.

Case B.2: Controllers with cell-internal compensatory fluxes and exponential time-dependent perturbations

The controllers are exposed to the same exponential perturbation profiles as in Fig 14. The exponential growth of V is written as $\dot{V}=\kappa ·V$, where κ (>0) is a constant and related to the doubling time of V given by ln 2/κ.

Fig 25a shows the performance of the motif 1 zero-order controller while Fig 25b shows the responses of the motif 1 antithetic controller. During exponential growth and constant k₃ the motif 1 zero-order and the antithetic controller show slight offsets from the theoretical set-point $A_{set}^{theor}$, while during phase 3 when both V and k₃ increase exponentially, both controllers break down. Besides their different kinetic implementation of integral control both the motif 1 zero-order and the motif 1 antithetic controller have analogous responses (for details, see S3 and S4 Texts).

Fig 25. Behaviors of the motif 1 zero-order, antithetic, autocatalytic and motif 2 zero-order controllers with internal compensatory fluxes in response to an exponential increase in V and k₃.

Time/perturbation profiles of V and k₃ are the same as in Fig 14. (a) Behavior of the motif 1 zero-order controller. Rate constant values as in Fig 18. Initial concentrations: A₀ = 2.0, E₀ = 4.0, V₀ = 25.0, M₀ = 4 × 10⁹, N₀ = 1 × 10⁶. (b) Behavior of the antithetic controller. Rate constants as in Fig 20. Initial concentrations: A₀ = 2.0, E_1,0 = 0.25, E_2,0 = 4.0, V₀ = 25.0, M₀ = N₀ = O₀ = 1 × 10⁶, Q₀ = P₀ = 0.0. During phase 2 the controller shows a slight but constant offset below $A_{set}^{theor}$. During phase 3 the controller breaks down when both V and k₃ increase exponentially. (c) Behavior of the autocatalytic controller. Rate constants are as described in Fig 22. Initial concentrations: A₀ = 2.0, E₀ = 4.0, V₀ = 25.0, M₀ = 4 × 10⁹, N₀ = 1 × 10⁷. During autocatalytic growth only (phase 2) the autocatalytic controller is able to move A_ss precisely to $A_{set}^{theor}$, but shows an offset from $A_{set}^{theor}$ when both k₃ and V increase exponentially). (d) Behavior of the motif 2 based controller (Eqs 62–66). Rate constants and initial conditions as in Fig 24. Note the significant overcompensation (offset above $A_{set}^{theor}$) during phase 2, but the return to $A_{set}^{theor}$ (=k₉/k₈) when k₃ starts to grow exponentially.

Fig 25c shows the response of the autocatalytic controller when $k_E^{in}=k_E^{out}=1\times {10}^{-5}$. The controller is able to keep A at $A_{set}^{theor}$ during exponential growth while k₃ is kept constant. Only when V and k₃ both increase exponentially then there is an offset from $A_{set}^{theor}$, which can be estimated as:

$$\begin{array}{c}\hfill A_{ss}=\frac{k_4}{k_6}-\frac{\kappa }{k_6}-\frac{\zeta }{k_6}\end{array}$$ (67)

where the theoretical set-point $A_{set}^{theor}=k_4/k_6$ and κ and ζ describe the doubling times ln 2/κ and ln 2/ζ of the exponential increases for V and k₃, respectively (see S5 Text).

In case $k_E^{in}$ and $k_E^{out}$ are large Eq 67 changes to (S5 Text):

$$\begin{array}{c}\hfill A_{ss}=\frac{k_4}{k_6}-\frac{\kappa }{k_6}-\frac{\zeta }{k_6}-\frac{k_E^{out}}{k_6}\end{array}$$ (68)

The motif 2 based controller shows in phase 2 a significant overcompensation from $A_{set}^{theor}$ when exposed to exponential growth only. The overcompensated steady state in A at constant k₃ and exponential growth can be expressed as

$$\begin{array}{c}\hfill A_{ss}=A_{set}^{theor}+\frac{\kappa }{k_8}{E}_{ss}\end{array}$$ (69)

where $A_{set}^{theor}=k_9/k_8$ and (κ/k₈)E_ss is the overcompensated offset (S6 Text).

The response kinetics of the motif 2 based controller is mostly determined by k₄, which reflects the derepression property by E. For large k₄ the derepression by E is observed to be slow and less effective.

Remarkably, when both k₃ and V increase exponentially in phase 3 the controller is able to move A close to $A_{set}^{theor}$. For this case A_ss can be written as (S6 Text)

$$\begin{array}{c}\hfill A_{ss}=\left(\frac{{\gamma }_0}{1+{\gamma }_0}\right)A_{set}^{app}\end{array}$$ (70)

where

$$\begin{array}{c}\hfill {\gamma }_0=\frac{k_4{k}_6{k}_8}{\dot{k_3}{(k_4+E\left(t\right))}^2}\end{array}$$ (71)

and

$$\begin{array}{c}\hfill A_{set}^{app}=A_{set}^{theor}+\frac{\kappa }{k_8}E\left(t\right)\end{array}$$ (72)

Note that during phase 3 E is not in a steady state, but decreases due to the controller’s derepression, while $\dot{k_3}$ increases exponentially. However, the derepression kinetics by E are faster than the exponential increase of $\dot{k_3}$ (Eq 71), such that γ₀ increases and $A_{set}^{app}$ and A_ss approach $A_{set}^{theor}$ (S6 Text).

Growth related to the surface to volume ratio and controllers with cell-internal compensatory fluxes

Here we show how the four controllers having cell internal compensatory fluxes perform with respect to a surface to volume ratio related growth law as found for spherical bacteria ([9, 10, 13], Eq 2). We consider again three phases as in the previous sections, but with the difference that V now grows according to Eq 2 with η = 1 and ξ = 0.2 (Fig 26a). The values of η and ξ are arbitrarily chosen. The outflow perturbation, described by k₃, is kept constant during phases 1 and 2, but increases exponentially during phase 3 (Eq 49). The response behaviors of the controllers towards increasing volume (when k₃ is kept constant) is initially very similar to that when V increases linearly. However, the motifs gain more and more control as $\dot{V}$ decreases, provided that there is sufficient material in the cell to generate enough E’s (for the motif 1 controllers) or that there is still sufficient E left (for the motif 2 controller) to keep the negative feedback loop operating.

Fig 26. Performance of the antithetic, autocatalytic and motif 2 based controllers towards surface/volume related growth in V and exponentially increasing outflow perturbation k₃ with cell-internal compensatory flux.

Rate constant values and initial conditions as in Fig 25.

As an example, Fig 26 shows the behavior of the motif 1 antithetic and autocatalytic controllers and the motif 2 zero-order controller when k₃ in phase 3 increases exponentially as described by Fig 14 and compensatory fluxes are generated cell internally. The motif 1 zero-order controller’s behavior (not shown) is again very similar in comparison with the motif 1 antithetic controller.

Overview of results

Tables 1 and 2 gives an overview of controller performances by dividing perturbations into (i) linear V only, (ii) linear V and k₃, (iii) exponential V only, and (iv) exponential V and k₃. Controller performances are described by the four categories perfect adaptation, partial adaptation, over-adaptation, and breakdown. Perfect adaptation means that the controller is able to keep A at $A_{set}^{theor}$. A controller with partial adaptation can maintain a constant A value during an applied outflow perturbation, but below $A_{set}^{theor}$. A controller showing over-adaptation keeps A above $A_{set}^{theor}$ even when the perturbation leads to a decrease in A. Controller breakdown means that the controller is unable to withstand the perturbation and A goes to zero.

Table 1. Performance of controllers based on internal generated compensatory fluxes.

controller type	linear V only	linear V and k3	exponential V only	exponential V and k3
m1—zero-order	perfect adaptation	partial adaptation	breakdown	breakdown
m1—antithetic	perfect adaptation	partial adaptation	breakdown	breakdown
m1—autocatalytic	perfect adaptation	perfect adaptation	perfect adaptation	partial adaptation
m2—zero-order	perfect adaptation	perfect adaptation	over-adaptation	perfect adaptation

Table 2. Performance of controllers based on transporter based compensatory fluxes.

controller type	linear V only	linear V and k3	exponential V only	exponential V and k3
m1—zero-order	partial adaptation	breakdown	breakdown	breakdown
m1—antithetic	partial adaptation	breakdown	breakdown	breakdown
m1—autocatalytic	perfect adaptation	perfect adaptation	partial adaptation	partial adaptation
m2—zero-order	perfect adaptation	perfect adaptation	perfect adaptation	perfect adaptation

Concerning the results with respect to surface/volume related growth we group this growth law together with the category of linear growth, because controllers behave initially quite similar towards these two growth laws (compare phases 2 in Fig 16b–16d with respective phase 2 behaviors of Figs 9, 11 and 13 and phases 2 in Fig 26b–26d with the phase 2 behaviors of Figs 20, 22 and 24, respectively).

Clearly, motif 1 controllers based on zero-order or on antithetic integral control, cannot oppose an exponential volume increase or when an additional exponential increase in k₃ is applied. When exponentially increasing perturbations are applied the motif 1 autocatalytic controller shows good performances with a stable offset in A below $A_{set}^{theor}$, but requires the presence of sufficient controller species E to maintain autocatalysis. The motif 2 controller using zero-order based integral control shows best performance, and is able to keep A at $A_{set}^{theor}$, even when both V and k₃ increase exponentially. However, the drawback of controllers based on derepression, like motif 2, is that controller breakdown occurs when concentrations of the derepressing control species is getting too low.

Discussion

Internal model principle and the kinetic limit of controllers

From Tables 1 and 2 it is seen that the motif 2 controller outperforms the other controllers. The derepression kinetics of the motif 2 controller is described by the term (Eqs 43 and 62):

$$\begin{array}{c}\hfill f_{inhib}\left(E\right)=\frac{k_4}{k_4+E}\end{array}$$ (73)

which is an essential part in generating the compensatory flux in A. For decreasing (derepressing) E f_inhib(E) increases with hyperbolic response kinetics, i.e. having exponentially increasing doubling times. The motif 2 controller is therefore able, as observed [18], to counteract hyperbolically decreasing concentrations in A. The balancing between a perturbation and the by the perturbation induced compensatory flux reflects the Internal Model Principle [25–27], which states that if a controller is able to oppose a perturbation, then the controller has the capability to generate that kind of perturbation internally. For the motif 2 controller the hyperbolic response kinetics represents the upper kinetic limit which the controller can handle. In addition, the motif 2 controller will handle any perturbing rate laws with doubling times lower than an exponential (constant doubling times relate to an exponential rate law), although overcompensation may occur as seen in Fig 25d.

Thus, as indicated in Tables 1 and 2 controllers group according to their kinetic limits, where the motif 2 controller with hyperbolic response kinetics performs better than controllers based on exponential/autocatalytic or linear responses.

Repression/derepression kinetics are ubiquitously used in homeostatic mechanisms (see Supplementary Material in [7]), in gene on/off regulations [28–30] and as rhythm generators [31, 32]. The fast response of derepression is also used in signaling [33], but may be needed to be kept under additional control as indicated in a study of the nitrogenase switch [30] to avoid overenhanced/overcompensated responses.

Breakdown of the motif 2 controller occurs when the compensatory flux has reached its maximum value (described by rate constant k₂ in Figs 12 and 23).

A somewhat surprising behavior of the motif 2 controller is its overcompensation when growth increases exponentially at constant k₃ (see phase 2 in Fig 25d). The overcompensation can be described analytically (Eq 69). Its origin is due to the fact that with a cell-internal compensatory flux an exponetial increase in V at constant k₃ allows for steady states in A and E, independent of V, where A_ss is larger than $A_{set}^{theor}$ (S6 Text).

Performance improvement by increased controller aggressiveness

Although the motif 1 zero-order and the antithetic controllers break down when exposed to exponential growth and perturbations (Figs 15a and 15b and 25a and 25b), their performance can be significantly improved at constant $\dot{V}$ by increasing of what can be described as the controllers’ aggressiveness. By aggressiveness of a controller we mean loosely the controller’s response to a perturbation in terms of (mainly) quickness and precision. Increasing the aggressiveness of a controller will generally lead to a quicker controller response and an improved controller precision.

The aggressiveness of an integral controller can be varied by the controller’s gain. The gain is a factor in front of the error integral. For an ideal motif 1 zero-order integral controller (working at constant V and k₃) $\dot{E}$ is proportional to the error $e=(A_{set}^{theor}-A)$ [7], i.e.,

$$\begin{array}{c}\hfill \dot{E}=k_6(\frac{k_4}{k_6}-A)\end{array}$$ (74)

where k₆ is the controller gain and k₄/k₆ is the controller’s theoretical set-point, $A_{set}^{theor}$. As indicated by Eq 74 the concentration of E is proportional to the integrated error with respect to time. By increasing k₆ and k₄ such that $A_{set}^{theor}$ remains unchanged the gain of the controller is increased and the controller becomes more aggressive.

For constant $\dot{V}$ and k₃ the steady state of A for the motif 1 zero-order controller is given by Eq 20

$$\begin{array}{c}\hfill A_{ss}=\frac{k_4}{k_6+\frac{2\dot{V}{k}_3}{k_2}}\end{array}$$ (20)

where the offset in A_ss below $A_{set}^{theor}$ is due to the term $2\dot{V}{k}_3/k_2$. This term indicates that for increasing $\dot{V}$ and/or increasing k₃ values the controller will break down and A will go to zero as observed in Fig 15a. There are two ways the controller’s aggressiveness can be increased. One way, as indicated above, is by increasing k₄ and k₆ such that $A_{set}^{theor}=k_4/k_6$ is preserved with k₆ becoming much larger than $2\dot{V}{k}_3/k_2$. As a result the controller’s response kinetics become quicker and A_ss moves closer to $A_{set}^{theor}=k_4/k_6$. The other way is to increase k₂, which means to increase the activity of the transporter. In a synthetic biology context this could be done by over-expressing the genes which code for the transporter. On the other hand, “normal” cells may already have optimized controller aggressiveness or may change it in response to environmental conditions.

Similar arguments apply also for the antithetic controller. Qian et al. [34] have shown that when the controller dynamics become faster than growth this leads to an improved controller performance.

Fig 27 shows the results of increasing the aggressiveness of the motif 1 zero-order and antithetic controllers by increasing k₂ from 1.0 to 1×10³. The perturbation is divided into three phases. During the first phase the volume V is kept constant at 25.0 and the controllers are at their set-points. In phase 2 the volume increases with a constant rate ($\dot{V}=1.0$). Finally, in phase 3 V continues to grow with $\dot{V}=1.0$ but k₂ is increased to 1×10³. Both controllers show improved precisions, but show different kinetics in their way to reach $A_{set}^{theor}$.

Fig 27. Increased transporter activity (k₂ values) lead to increased aggressiveness and improved controller precision for transporter-based motif 1 zero-order controller (left panel) and motif 1 antithetic controller (right panel) during constant growth (see Figs 6 and 8).

Phase 1: controllers are at their steady state, no growth, k₂ = 1.0. Phase 2: constant growth ($\dot{V}=1.0$) and k₂ = 1.0. Both controllers show an offset in A_ss below $A_{set}^{theor}$. Phase 3: constant growth continues but k₂ is increased to 1 × 10³. Both controllers show improved precision and have their A_ss close to $A_{set}^{theor}$, but show different adaptation kinetics during the transition from phase 2 to phase 3. Rate parameters and initial concentrations, zero-order controller: k₃ = 2.0, k₄ = 20.0, k₅ = 1 × 10⁻⁶, k₆ = 10.0, k₇ = 1 × 10⁻⁶, A₀ = 2.0, E₀ = 100.0, V₀ = 25.0, M₀ = 1 × 10⁷. Rate parameters and initial concentrations, antithetic controller: k₃ = 2.0, k₄ = 10.0, k₅ = 1 × 10⁻⁶, k₆ = 10.0, k₈ = 20.0, k₉ = 1 × 10⁻⁶, A₀ = 2.0, E_1,0 = 1 × 10⁻², E_2,0 = 1 × 10², V₀ = 25.0, M₀ = O₀ = 1 × 10⁸.

Similar is the situation when the compensatory flux is internally generated. Eq 55 shows the steady state in A for the motif 1 zero-order controller. Also here increasing k₂ values will move A_ss towards the theoretical set-point $A_{set}^{theor}=k_4/k_6$.

Aggressiveness can also be increased for the autocatalytic controller by increasing k₄ and k₆ such that the k₄/k₆ ratio is maintained. This will move the steady state in A closer to its theoretical set-point as offsets become smaller (Eqs S14 and S20 in S5 Text).

Roles of kinetic implementations of integral control and negative feedback structures

For the transporter-based cases the increased aggressiveness of the motif 1 zero-order and antithetic controllers allows them to defend their theoretical set-points as long as (see Eqs 20 and 29)

$$\begin{array}{c}\hfill k_6\left(\text{or}{\text{k}}_4\right)\gg 2\dot{V}\left(\frac{k_3}{k_2}\right)\end{array}$$ (75)

However, for exponentially increasing V and $\dot{V}$ this can be achieved only for a certain (often short) time period. The motif 1 zero-order controller will break down when Eq 75 is no longer fulfilled. On the other hand, as shown above, the autocatalytic motif 1 controller is able to maintain a stable steady state in A, although with an offset from $A_{set}^{theor}$, when V and k₃ increase exponentially (but also here dependent on the controller’s aggressiveness). As Eq 38 (for the transporter-based compensatory flux) indicates, any time-dependent perturbation of the type k₃(t) = k_3,0 + a⋅tⁿ (a, n > 0) will be successfully defended by the autocatalytic controller, because $\dot{k_3}/k_3\to 0$ (S5 Text) and thereby restoring the controller’s theoretical set-point. However, breakdown may occur if no sufficient supply of E (for example via M, Fig 11) can be maintained.

The sudden breakdown of a fully adapted controller due to capacity limits or exhaustion of the controller variables E or E₁/E₂ has an interesting analogy in physiology described by Selye’s General Adaptation Syndrome (GAS) [35]. When an animal is exposed to constant but severe stress (for example cold temperatures) the animal can stay, after an alarm reaction, in a stage of resistance, where the animal appears perfectly adapted to its environment. However, after a certain time there appears the stage of exhaustion and the animal dies, despite of sufficient food supplies. To understand the sudden and unexpected breakdown of adaptation, Selye introduced the concept of adaptation energy [36]. In our analogous examples here, the adaptation energy can be associated with the amounts of precursors M, N, and O, and with the maximum controller capacity, described by the maximum rate a compensatory flux can deliver. Although our single loop controllers are a far cry from a physiologically regulated system, the analogy to Selye’s GAS is thought-provoking.

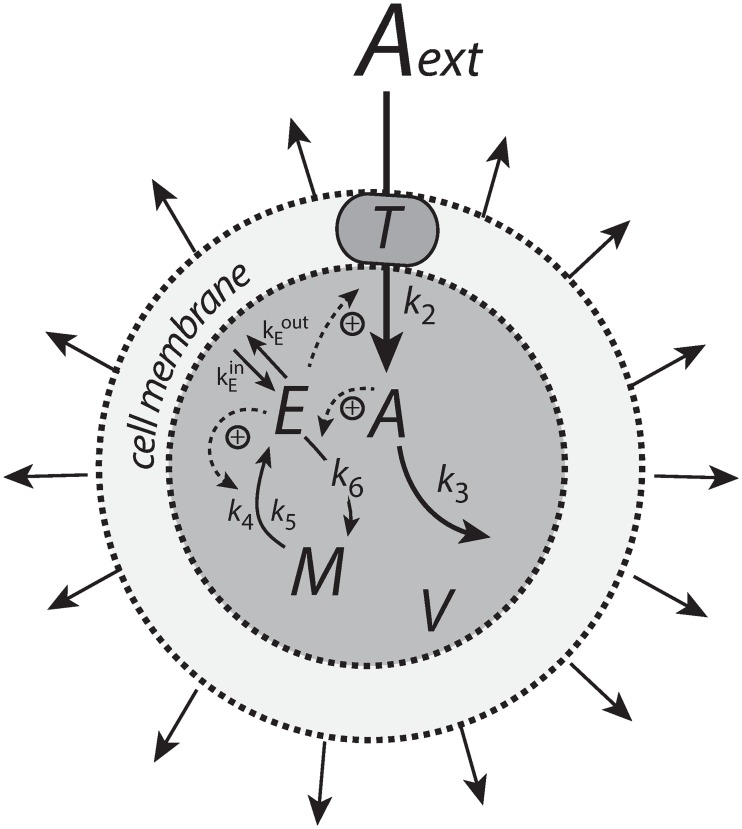
Our results indicate that the type of kinetics realizing integral control and the structure of the negative feedback loop play essential roles in how a controller will perform. The antithetic integral controller has in the literature [22, 37, 38] so far only been considered in a motif 1 setting based on activation (Fig 1). However, its second-order integral controller part can be embedded into other feedback structures (S7 Text). Although the intension of this work was not to consider novel implementations of the antithetic integral controller, it is illustrative to see the controller’s improvement and limitations when considering the antithetic controller in a motif 2 background. Fig 28 shows two such implementations, one with a transporter based compensatory flux and the other with a cell internal one.

Fig 28. Antithetic integral controllers with motif 2 feedback structure and transporter based and cell internal compensatory fluxes.

When merging the motif 2 structure with the antithetic integral controller, we keep the antithetic controller’s rate constant values, but change the k₂ and the inhibition constant (k₁₀) values to those used in the motif 2 controller calculations. For the transporter based motif 2 antithetic controller Eq 21 is now replaced by

$$\begin{array}{c}\hfill \dot{A}=\frac{k_2·k_{10}}{k_{10}+E_1}·\frac{1}{V}-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (76)

while for the controller with a cell internal compensatory flux, Eq 56 is replaced by

$$\begin{array}{c}\hfill \dot{A}=\left(\frac{N}{k_7+N}\right)·\left(\frac{k_2{k}_{10}}{k_{10}+E_1}\right)-k_3·A-A\left(\frac{\dot{V}}{V}\right)\end{array}$$ (77)

The other rate equations (Eqs 22–27) remain unchanged. Fig 29 shows the results when linear and exponential growth and k₃ changes (see Figs 9a and 14) are applied to the controllers in Fig 28.

Fig 29. Performance of the antithetic controller in a motif 2 (m2) structural background (Fig 28).

(a) The controller has a transporter mediated compensatory flux and is exposed to linear growth and increase in k₃ as in Fig 9a. Same rate constants and initial concentrations as in Fig 9 with the exception that k₂ = 1 × 10⁵, and k₁₀ = 1 × 10⁻³. Note the minor offset in A during phase 2. (b) Same controller with rate constants as in (a), but exposed to exponential volume and k₃ increases as in Fig 14. Initial concentrations: A₀ = 2.0, E_1,0 = E_2,0 = 1.0, M₀ = O₀ = 1 × 10⁵. The controller is not able to oppose exponential growth. (c) Controller with a cell internal compensatory flux (Fig 28) and exposed to the conditions as in Fig 20. Same rate constants as in (a). Initial concentrations: A₀ = 2.0, E_1,0 = E_2,0 = 25.0, M₀ = O₀ = 2 × 10⁵, N₀ = O₀ = 1 × 10⁶. The controller is fully capable to oppose linear growth together with a linear increase in k₃. (d) Same controller with rate constants as in (c), but exposed to exponential volume and k₃ increases as in Fig 14. Initial concentrations as in (c), but to avoid depletion of M and O initial concentrations of these compounds were raised to 1 × 10⁶. Note also here the overcompensation in the case growth occurs exponentially in phase 2. Despite the larger consumption rates of M and O in comparison with (c) the controller is not able to counteract both exponential increases in V and k₃. See S7 Text for more details.

In comparison with the motif 1 antithetic structure, the usage of the motif 2 negative feedback shows a clear improvement in the antithetic controllers’ performance (compare Fig 29a, 29b, 29c and 29d with Figs 9, 15, 20 and 25, respectively). The feedback design based on a cell internal compensatory flux shows again a better performance in comparison when the compensatory flux is transporter based. On the other hand, when both V and k₃ increase exponentially both motif 2 antithetic controllers are not able to keep A at a constant steady state. The reason for this is that the rate of derepression/removal in E₁ is limited by its reaction with E₂ and thereby is slower than the E removal in the motif 2 zero-order case.

From a biochemical perspective one may question how realistic a second-order removal of E₁ and E₂ is. Since practically all physiological reactions within a cell are catalyzed by enzymes, it appears to be an interesting alternative to study the performance of controllers when an enzyme uses E₁ and E₂ as substrates.

With respect to the autocatalytic implementation to achieve integral control [19–21], the occurrence of autocatalysis and positive feedback loops are becoming more and more recognized in signaling and homeostatic regulation [39–41]. As an illustration, in cortisol homeostasis ACTH signaling from the brain-pituitary system to the cortisol producing adrenals occurs by autocatalysis/positive feedback [42]. In blood sugar homeostasis insulin secretion is activated by several positive feedback/autocatalytic signaling pathways [43–45] to ensure an effective regulation in glucose concentration. These examples indicate the importance of additional “helper kinetics” (such as autocatalysis/positive feedback) to obtain a homeostatic regulation with optimum response and precision properties. For synthetic biology this means that knowledge about controller structure and their inherent kinetics are important aspects in the design and implementation of artificial regulatory units when trying to oppose the dilution effects of growth or other time-dependent perturbations.

Outlook

The approach taken here is based on ordinary mass action kinetics and thereby is purely deterministic. In addition, we made the assumption that the cellular volume is well-mixed and homogenous. Both assumptions are subject to certain criticism, when applied to biochemical reactions within a cell. While in many cases a chemically reacting system can be treated as a continuous deterministic process, in other cases, in particular when the number of reacting molecules becomes low, reactions may better be described as discrete stochastic processes [46–48]. However, many, if not most of the stochastic approaches to describe cellular processes still treat (and require) that systems are treated as homogenous, thereby neglecting “recruiting” or “funneling” mechanisms which occur, for example, on the surface of cellular membranes, involve multiprotein complexes (“antenna”) in photon harvesting [49], or use substrate channeling (“tunnels”) in enzyme-catalyzed reactions [50].

Ignoring these spatial aspects, it may be mentioned, that the controller motifs 1 and 2 (Fig 1) based on zero-order and first-order autocatalysis are well-described by the Gillespie algorithm [46] and show an excellent correspondence between the stochastic and deterministic approach (P. Ruoff, unpublished results). The motif 1 antithetic controller has been shown to work well under stochastic conditions by exploiting noise, and achieves regulation where a similar deterministic approach apparently fails [21]. How these controllers behave under time-dependent perturbations and stochastic conditions is an interesting aspect which we would like to investigate in a later work.

Nevertheless, we feel that the deterministic calculations presented here give a first ranking between the various integral controllers when exposed to different growth laws and dilution kinetics.

Supporting information

S1 Matlab. A set of Matlab files showing the results of Figs 4, 7, 9, 11, 13, 15, 18, 20, 22, 24, 25, 26 and 27.

(ZIP)

S1 Text. Steady state of cell-internal-generated compound A without negative feedback.

(PDF)

S2 Text. Steady state of transporter-generated compound A without negative feedback.

(PDF)

S3 Text. Steady states and theoretical set-point for motif 1 zero-order controller.

(PDF)

S4 Text. Steady states and theoretical set-point for motif 1 second-order (antithetic) controller.

(PDF)

S5 Text. Steady states and theoretical set-point for motif 1 autocatalytic controller.

(PDF)

S6 Text. Steady states and theoretical set-point for motif 2 zero-order controller.

(PDF)

S7 Text. Novel antithetic integral controller arrangements and steady states in a motif 2 background.

(PDF)

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

This research was financed in part by Program Area Funds from the University of Stavanger to PR and TD. There was no additional external funding received for this study. The University of Stavanger (funder) had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.