Abstract
In this tutorial, we introduce basic concepts in dynamical systems analysis, such as phase‐planes, stability, and bifurcation theory, useful for dissecting the behavior of complex and nonlinear models. A precursor‐pool model with positive feedback is used to demonstrate the power of mathematical analysis. This model is nonlinear and exhibits multiple steady states, the stability of which is analyzed. The analysis offers insight into model behavior and suggests useful parameter regions, which simulations alone could not.
Mechanism‐based and systems pharmacology‐based models are increasingly used in the pharmacological studies.1, 2 These models are increasingly complex and are based on differential equations (DEs). DE‐based models have been used in physics, engineering, and biology for a long time, for example, to model motions of objects, transfer of heat, as well as cell cycles and firing of neurons. Well‐developed mathematical and computational methods exist for solving (where possible), analyzing the dynamics of, and simulating the DE‐based models. Computational methods play a big role in simulating such models, but may offer only a limited picture of model behaviors, particularly for nonlinear models. Nonlinear models can exhibit rich and counterintuitive behaviors, which can be difficult to understand through simulations alone. Mathematical techniques, such as dynamical systems analysis, on the other hand: (1) provide better insight into the behavior of these models; (2) show how many steady states a model has and which ones are stable, which may allow us to reject a model even before any data fitting is performed; (3) allow predicting which regions of parameter space provide meaningful results (for example, stability for required steady states); (4) suggest ways in which a model can be reduced or altered to better describe the biological system at hand, and (5) predict the outcome of simulations, which helps in verifying and understanding simulation results.
Rich literature exists in the field of mathematical biology in which these techniques are applied to complex and nonlinear models of biological systems.3, 4, 5, 6 Usually, these models are mechanism based in that they are built on knowledge of the underlying mechanical, physical, or biological system. In pharmacology, however, the underlying system is often only partially understood and models are based on a mix of biological and physiological information as well as experimentally obtained data. This raises new questions, such as the validity of the model under conditions for which no data are available, and often experiments are designed to challenge a proposed model.
In order to demonstrate all the working steps in a typical dynamical systems analysis in a pharmacological context, we focus this tutorial on a specific case study: the response of prolactin (PRL) to antipsychotic drugs, and, specifically, a model that has been used to account for this response. This model is based on the classical “precursor‐pool model.” We have deliberately chosen this simple model as a starting point because it is a turnover model. Such models are ubiquitous in pharmacology, and therefore more familiar to a pharmacologist than some of the mathematical biology models. We would like to emphasize, though, that the techniques presented here are applicable to a wide range of DE‐based models. Precursor‐pool models have been in use in the pharmacokinetic (PK) pharmacodynamic (PD) literature for a long time and are used to explain the tolerance and rebound components of a drug response.7, 8, 9, 10, 11 These are precursor‐dependent indirect response models, which assume that the tolerance (or rebound) results from depletion (or accumulation) of finite pools of precursors that are responsible for the drug effect. The pool model has been applied to the PRL response after administration of antipsychotic drugs, in order to explain the tolerance after repeated drug administration at closely spaced intervals. To account for the effect of an antipsychotic drug (remoxipride) in rats, the original PRL pool model8 was modified by ref. 12 to include a positive feedback (PF) component. The modified model is nonlinear. When the same model is used to study the effects of risperidone in rats, simulations find that the model predicts one PRL baseline for some doses but a higher baseline for other doses (discussed further below). With mathematical analysis we are able to understand precisely why the model shows this behavior. Moreover, we are able to predict this counterintuitive behavior through analysis. Without this insight one would have to rely on serendipitous discovery of such behavior through simulations.
We begin this tutorial by presenting some basic steps in the dynamic analysis of ordinary differential equation (ODE) models, using the basic precursor‐pool model as an example. We demonstrate the process of the determination of steady states followed by nondimensionalization. We then illustrate the phase‐plane analysis, which is a transparent geometric tool to gain insight into the dynamics of two‐ODE systems. We then apply these techniques to the pool model with PF to understand the counterintuitive behavior in an apparently simple ODE model. We further use this model to demonstrate concepts, such as bifurcation analysis, for determination of parametric dependence of stability properties of a model, and to explain the counterintuitive behavior shown by the pool model with PF.
DYNAMICAL SYSTEMS ANALYSIS OF ODE MODELS—A STEP‐WISE GUIDE
In this tutorial, we focus on small models with two ODEs. We present the analysis within the framework of a specific example, the classical “precursor‐pool model” in pharmacology.10
Precursor‐pool model
The typical precursor‐pool model describes the dynamics of two quantities, referred to as the “precursor” often denoted by “P” and the “response” denoted by “R.” It is based on the assumption that there is a finite pool of precursors, which produces the response. Thus, it is a two‐compartment model involving a precursor pool and a response compartment. The dynamics of a pool model is described by the system of DEs:
| (1) |
| (2) |
Here P denotes the precursor concentration in the pool, R the response, ks the synthesis rate of precursors, kr the release rate constant of precursors, and kel the elimination rate constant of the response. Note that Eq. (1) is identical to the widely used indirect response model.
A steady state of a system is a state that is constant in time (i.e., rate of change of all variables is zero). Let P 0 and R 0 denote the steady state concentrations of P(t) and R(t), respectively. Then we conclude upon substitution into the system (Eq. (1)) that:
| (3) |
Solving this pair of algebraic equations, we obtain the following expressions for P 0 and R 0:
| (4) |
Step 1: Nondimensionalization
Nondimensionalization is the process of converting a model with dimensional variables and parameters into one that has dimensionless variables and parameters. This process typically reduces the number of parameters in the model by grouping some of them together. The applications of this approach in the PK‐PD literature can be found in refs. 13 and 14.
There are several advantages of using the nondimensional form of a model:
The nondimensional system is often simpler, whereas it still retains the dynamical structure of the original model.
The nondimensional model contains fewer (dimensionless) parameters that determine the characteristic features of the dynamics described by the model.
The nondimensional variables and parameters can be compared to each other through their magnitudes. By contrast, the dimensional quantities, which may have different units, cannot be compared meaningfully with each other.
Choosing alternate time and concentration scales can also allow one to zoom into various subprocesses making up the dynamics of the system. Thus, the presence of different time scales in a model can be exploited to obtain simplified models that describe a particular aspect of the dynamics, such as a startup, a transition, or large‐time behavior. Segel and Slemrod15 nicely illustrate the tasks and challenges of nondimensionalization using the Michaelis‐Menten reaction kinetics. For examples in which different time and concentrations ranges are used to dissect complex models, we refer to Schmidt et al.14 and Peletier et al.16
Making the system dimensionless involves comparing the variables to conveniently chosen reference values. Thus, for the precursor‐pool model, the steady state values, also referred to as baseline values, P 0 and R 0 can be used to define corresponding dimensionless variables u and v:
We have yet to choose an appropriate reference value for the time. Suitable candidates are the turnover times of the first or the second equation (i.e., or ). Using as a reference time we substitute
Thus, the dimensionless variables are defined by:
| (5) |
They yield the dimensionless system of:
| (6) |
| (7) |
where α, is a dimensionless constant that is the ratio of the two time scales in the model, the one for the pool compartment ( ) and one for the response compartment ( ):
We see that the dimensionless model (Eqs. (6) and (7)) has just one parameter, as compared to three in the original model (Eqs. (1) and (2)). Thus, for different values of kr and kel with the same ratio α, plotting the scaled concentrations results in identical plots, rather than plotting the dimensional concentrations.
Plainly, by the definition of the dimensionless variables u and v, the steady state of the dimensionless model is:
Note that we could equally well have chosen as a reference time. This would have yielded a slightly different dimensionless system: the parameter α in the first equation would have disappeared, while a parameter would have appeared as a factor of in the second equation.
Step 3: Phase‐plane analysis
The “phase‐plane” is a geometric representation of the dynamics of a two‐dimensional system of ordinary differential equations and is a useful tool for acquiring insight into the global and local dynamics of the system.
Points in the (u, v)‐plane represent states of the system, and Eqs. (6) and (7) uniquely determine its subsequent behavior. As time progresses, the state traces a trajectory in the phase plane, which is also called an “orbit.” The velocity —speed and direction—is defined by the state (u, v) through the DEs:
Thus, at every point in the phase plane, the DEs define a direction of the velocity field.
In analyzing the behavior of the solution orbits, two curves are especially useful: the curves along which the vector field is vertical (i.e., (Γu)) and the curves along which it is horizontal (i.e., (Γv)). In other words, Γu and Γv each denote a curve along which the rate of change of u and v is zero, respectively. They are called the “null clines” of the system. Using Eqs. (6) and (7), we find that they are given by:
| (8) |
| (9) |
Plainly, points where the null clines intersect are the steady‐state points. In this example, we see that there exists a unique point of intersection . A given null cline divides the phase plane in two different regions: one where the rate of change of the respective variable is positive and one where it is negative. In the phase plane of the pool model, shown in Figure 1 a, Γu divides the plane such that on its left‐hand side the rate of change of u is positive (indicated by the green rightward arrows, and on its right side the reverse is true (green leftward arrows). These directional arrows are obtained by studying the respective differential equation. Similar arguments apply to Γv. The directions of change of v in these two regions are indicated by blue downward and upward arrows. Thus, the two null clines divide the plane into four regions, denoted here by I, II, III, and IV, each with a distinct resultant vector direction. In region I, the velocity vector q points SE (↘), in region II it points SW (↙), in region III NW (↖) and in region IV NE (↗). In Figure 1 a, we show the directions of the vector field in the four regions schematically.
Figure 1.
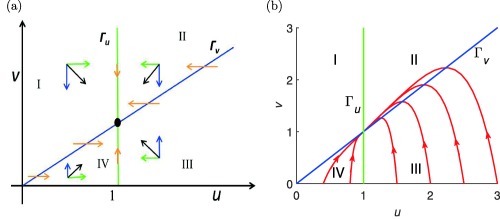
(a) Directions of the vector field in the four regions I, II, III, and IV in the phase plane divided by the null clines Γu (green) and Γv (blue). Please refer to the text for description of the blue and green arrows. (b) Orbits in the phase plane for starting at where u(0) = 0.4, 0.8, 1.5, 2.0, 2.5, 3.0, and , as well as the null clines Γu (green) and Γv (blue) (MATLAB model code provided in Supplementary Figure S1).
In Figure 1 b, we show orbits of the system (Eqs. (6) and (7)) for starting at the points , where 0.4, 0.8, 1.5, 2.0, 2.5, 3.0, and , together with the null clines Γu (green) and Γv (blue). They all converge to the unique steady state point . We note that the orbits cross Γv horizontally and do not cross Γu.
In pharmacology, dependent variables often represent concentrations that cannot become negative. It is possible to use the phase plane to determine whether a model is likely to predict negative concentrations. We encourage readers to work through Exercise A.1 in order to determine whether P and R may become negative in this example.
Orbits do not intersect
Observe that the orbits shown in Figure 1 a do not intersect. This is a general property of autonomous systems (i.e., systems in which the time variable does not appear explicitly), as is the case in the pool model (Eqs. (6) and (7)), where the right‐hand sides are functions of the dependent variables u and v only. In contrast, if a parameter depends upon time, for example, in case of a drug‐effect component, which changes in response to drug concentration changes in time, then the system is not autonomous any longer.
Suppose to the contrary that two orbits intersect at a point Q. Then Q would be the starting point for two different orbits when we let time run backward. This contradicts the uniqueness property. The uniqueness property requires that when the right‐hand sides of the system of DEs are smooth functions of the dependent variables, as they are in the system of Eqs. (6) and (7), then through every point (u,v) the phase plane passes one and only one orbit.
Orbits do not cross Γu
We observe in Figure 1 a that although orbits cross the null cline Γv, they do not cross the null cline Γu. The reason is that Γu is not only a null cline but also an orbit (see exercise A.2).
Stability
We note that the arrows in the phase plane all point to the unique stationary point . This suggests that this point is stable, in fact asymptotically stable in that:
| (10) |
We observe that as the orbits—whether from above or below—converge upon the stationary point (1,1), they are ultimately tangent to the null cline Γv. In Figure 2 a, we demonstrate that this property is related to the value of α and changes as α become large.
Figure 2.

(a) Orbits in the phase plane for and α = 10 starting at . Both orbits converge toward the unique steady state but, depending on α, along very different routes (MATLAB model code provided in Supplementary Figure S2). (b) Graphs of the functions (in red) and (in blue) which solve Eqs. 13 and 14 for α = 10.
Impact of the parameter
If α ≫ 1, then kr ≫ kel and quickly moves to its null cline Γu, much faster than . Therefore, the orbit will reach its limit point from below. On the other hand, If α ≪ 1, then kr ≪ kel and the inequalities are reversed. Now quickly moves up toward its null cline Γv while moves relatively slowly. Note that orbits in region III can leave region III and enter region IV before converging to the steady state for . However, if orbits begin in region II (or IV), they must stay in region II (or IV), regardless of the value of α (see exercise A.3).
Quasi‐steady state
In pharmacology, it is not uncommon that time scales are very different, for instance that kr ≫ kel or, conversely, kr ≪ kel. In such a situation, it is possible to reduce the system to a simpler one because the two quantities rapidly reach a quasi‐steady state and then together move slowly toward the final steady state. A classic example of the application of quasi‐steady state approximation to a biochemical reaction is the derivation of the Michaelis‐Menten equation in enzyme kinetics.15 However, in this tutorial, we briefly introduce the method using the example of the pool model.
Suppose that kr ≫ kel and hence α ≫ 1. When we divide the first equation by α and write , we obtain:
| (11) |
This is a classic “singular perturbation problem.” Following standard theory,17 we may conclude that very quickly jumps to its limit value u = 1 (while hardly moves) and then stays there—in quasi‐equilibrium—for all later time. Thus, we may then approximate the system (Eq. (11)) by the reduced system:
| (12) |
Thus, after this initial jump, we have to good approximation and the function solves the equation:
| (13) |
This equation can be solved explicitly: for the solution is given by:
| (14) |
In Figure 2 b, we show graphs of the solutions and of the Eqs. (13) and (14) when the initial data are and for α = 10 (i.e., ). Notice the rapid initial jump of the function , so that for most of the interval over which converges to its limit 1 (i.e., for most of the time, the first Eq. of 11) was in a quasi‐equilibrium or quasi‐steady state.
Arguments, such as used above, for α large can also be used when α is small (i.e., when kr ≪ kel).
SUMMARY AND DISCUSSION
We have explained how the dynamic and steady‐state behavior of a system of two ordinary first‐order DEs can be studied by going through steps of finding steady states, introducing dimensionless variables and analysis of the orbits in the phase‐plane, yielding insight into issues of stability, and parameter dependence. As a case study, the classic precursor‐pool model has been used. This model consists of two linear turnover equations in the dependent variables only, and thus has a unique steady state.
In the next section, we present a case study in which these steps are applied to two modified pool models that have been used by, respectively, refs. 8 and 12 in the study of the Lactotroph‐Prolactin system. This introduces two new elements: (i) the impact of a drug on the system, which causes some of the coefficients to depend on time t, and (ii) nonlinearity because of a positive feedback loop in the system. Here, this results in multiple steady states.
PROLACTIN BEHAVIOR IN THE BODY: APPLICATION OF THE POOL MODEL
PRL is a polypeptide hormone with a primary role in regulation of lactation in humans. PRL is predominantly secreted by specialized cells in the anterior pituitary gland called the lactotrophs.18 Antipsychotic drugs, such as remoxipride, chlorprothixene, and risperidone, stimulate the release of PRL in the blood, which leads to side effects, such as galactorrhea and menstrual disturbances.19
It has been observed that the interval between two doses of an antipsychotic medication determines the intensity of the PRL response in plasma. For closely spaced doses, the response to the second dose is lower than that to the first dose, whereas for widely spaced dosing intervals, both the responses are of comparable intensity. In order to investigate this phenomenon further, eight healthy male volunteers were given two doses of the drug remoxipride at various intervals. The resulting plasma PRL response was measured.20 Results showed that for 8 and 12‐hour intervals, the plasma PRL peak following the second dose is smaller than the first, whereas for a 48‐hour interval both the doses elicit peaks of comparable intensity (see Figure 1 in ref. 20 and Figure 4 in ref. 8).
Figure 4.
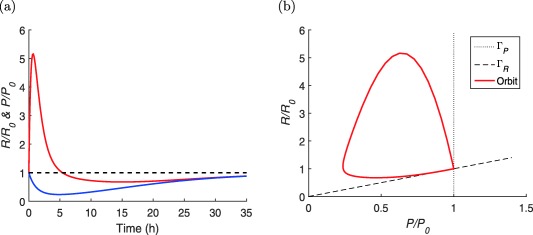
(a) Graphs of R(t) (red) and P(t) (blue), normalized with respect to their baseline values R 0 and P 0, of the system (Eqs. 15 and 16) for system parameters ks = 26 ng ⋅ mL−1 h−1, and kel = 2.2, h−1 and pharmacokinetic (PK) data Smax = 66 and for D = 3, h−1 ( and ng ⋅ mL−1). (b) The same simulation plotted in the phase plane (MATLAB model code provided in Supplementary Figure S4).
In ref. 8, a precursor‐pool model has been proposed to explain the observed dampening of the PRL response in plasma with a precursor compartment for lactrotroph PRL and a central compartment for plasma PRL. When a stimulatory drug is administered it increases the release of PRL from lactotrophs. Figure 3 a shows the schematic representation of the pool model.
Figure 3.
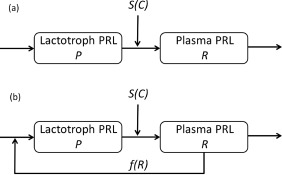
(a) Schematic representation of the precursor‐pool model for prolactin (PRL) response involving a drug‐intervention through the stimulatory drug effect function S(C) on the elimination of PRL from the lactograph compartment. (b) Schematic representation of the modified pool model for PRL response, involving a positive feedback of the PRL concentration in the plasma compartment on the PRL‐production rate in the lactograph compartment modeled by a nonnegative nondecreasing function f(R).
A drug challenge leads to the depletion of the PRL pool as the zero‐order PRL synthesis rate in the lactotroph compartment is unable to quickly replenish the pool. This leads to the reduction in intensity of the response to the subsequent closely spaced drug challenges. Eqs. (15) and (16) describe the dynamics of PRL concentration in the lactotroph and the plasma compartment, respectively, in the presence of a drug.
| (15) |
| (16) |
Here, P denotes the lactotroph PRL concentration, R denotes the plasma PRL concentration, and S(C) denotes a relation between drug concentration and the degree of stimulation of PRL release. Various functional forms for S(C) were tested by the authors and the maximum effect (Emax) function was found to be the most suitable.8 Thus, the following equation:
| (17) |
In the absence of a drug (i.e., when C = 0), Eqs. (15) and (16) are identical to Eqs. (1) and (2), as presented in an earlier section above. Thus, from the analysis we presented, we know that the PRL pool model has a unique steady state (P 0, R 0) given by:
| (18) |
and that this steady state is asymptotically stable.
In Figure 4 a, we show a simulation of the concentrations R and P, respectively, in the prolactin and the lactograph compartment according to the model in Eqs. (15) and (16) with parameter values of ref. 8. In this simulation, a simple mono‐exponential drug concentration has been used. The concentrations are normalized with respect to their baseline values R 0 and P 0 in order to compare them. Figure 4 b shows the same simulation plotted in a phase plane. The null clines for R and P are also normalized with R 0 and P 0.
The pool model is a simple linear model and lacks physiological and mechanistic detail. Stevens et al.,12 modified the pool model to incorporate the experimentally observed interaction between plasma PRL and the PRL synthesis rate in lactotrophs. In the next section, we study the impact of this positive feedback on the PRL synthesis rate.
Pool model with positive feedback
Stevens et al.12 applied the pool model to repeated remoxipride challenge data from rats. They found that when the two remoxipride doses are closely spaced, the original pool model (which was developed using clinical data) leads to slight overprediction of PRL response to the second drug challenge. As preclinical data are richer than clinical data, it is possible that mechanistic (complex) models are needed to explain the data, whereas simpler models are adequate for the more limited clinical data. Stevens et al.12 argued that a variable PRL synthesis rate (ks) could be necessary to obtain a better fit (personal communication). Experimental evidence suggested that PRL may regulate its own synthesis rate in lactotrophs. It has been shown that the plasma PRL signals through cell‐surface receptors present on the lactotrophs via the JAK/STAT pathway.21 PRL has also been shown to signal via the MAPK pathway.22 Estrogen, which is an endogenous stimulator of PRL synthesis, also signals through the MAPK pathway.21, 23 Thus, Stevens et al.12 hypothesized that the signaling that ensues following binding of PRL to PRL receptors on lactotrophs may result in the increased synthesis of PRL in the lactotrophs in a positive‐regulatory manner. Authors postulated that an increase in plasma PRL levels could function as an indicator of the emptying of the pool. Hence, they argued that increased plasma PRL levels may positively regulate the PRL synthesis rate in the lactotrophs in order to replenish the pool. Thus, they modified the pool model by adding a positive feedback (f(R)) in the form of an Emax function and showed that the modified model fits data from the remoxipride challenge in rats well.12 Figure 3 b shows the modification of the pool model due to the addition of the positive feedback denoted by f(R).
The equations for the modified pool model are:
| (19) |
| (20) |
Here, the function f(R), which models the positive feedback, is defined by:
| (21) |
The positive feedback is considered to be only active when . This condition—in ref. 12 referred to as the “if condition”—is incorporated as a Heaviside function , which is simply a mathematical representation of the “if condition” used by authors. Thus, for and for . The functional form of S(C) is given by Eq. (17), as in the case of the original pool model.
Stevens et al.12 used the model given by Eqs. (19) and (20) to fit plasma PRL response shown by rats to repeated remoxipride challenge at various dosing intervals. The parameter estimates obtained from this model fit are listed in Supplementary Table 1. As in case of human subjects, the dosing interval plays a role in determining the intensity of the response to the second drug challenge. In case of rats, however, the time scale is different to that in humans. Furthermore, the drug PK in humans and in rats also occurs on different time scales owing to the interspecies differences.
Counterintuitive behavior
When Drs. Proost and Taneja attempted to use the PK model developed by Kozielska et al.24 to drive the positive feedback model given by Eqs. (19) and (20) to model the risperidone challenge data in rats, they observed counterintuitive behavior of the PRL response (private communication). Specifically, they found that, depending on the drug dose D, the PRL concentration R converged to different steady state (or baseline) values. For example, for doses 0.05 and 2 mg/kg, the plasma PRL levels return to R 0, whereas for doses 0.1 and 1 mg/kg they reach a higher value at steady state (cf. Figure 5). We also point out that even in the absence of any drug, the plasma PRL settles at a higher steady state rather than the baseline R 0 value, which would be expected from the original pool model.8 This raised the question “why R eventually reaches R 0 steady state for some doses, whereas for other doses it reaches a higher steady state in the simulations.” Note that in vivo the existence and approach to a higher steady state has not been observed. Note also that the steady state value reached in these simulations does not monotonically increase with drug dose.
Figure 5.
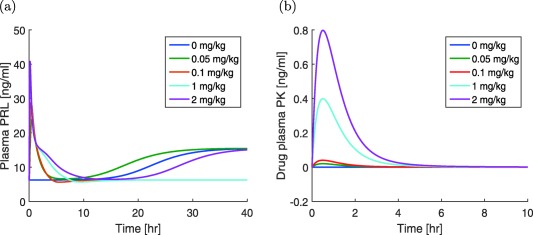
(a) Counterintuitive dose‐dependent steady‐state response displayed by the modified pool model of prolactin (PRL) response with positive feedback. Note that all the simulations are started in the neighborhood of the steady state from the linear pool model,8 which is also the desired steady state after the addition of the positive feedback. (b) The plasma pharmacokinetic (PK) shown by the drug simulated using the PK model for s.c. dose of risperidone24 (MATLAB model code provided in Supplementary Figure S5)
It is interesting to note that when the PRL concentration converges to the baseline R 0, it does so from below (i.e., the concentration first drops below the baseline and then converges monotonically toward it).
Nondimensionalization
In the following sections, we present the analysis of this model without the inclusion of the “if condition” in order to understand the behavior of the model. We have already identified the units of all variables and parameters in the model (Supplementary Table 1). P 0 and R 0, as given in Eq. (18), is the expected steady state of this model. Therefore, we use P 0 and R 0 to nondimensionalize the lactotroph PRL and plasma PRL concentrations, respectively. Thus, the nondimensionalization scheme is:
| (22) |
Thus, the nondimensionalized equations are:
| (23) |
| (24) |
where denotes the drug effect, which can vary as a function of time, depending upon the drug PK.
Steady‐state analysis
While considering steady states, we need to remember that the parameter depends on time as it incorporates drug PK C(t). For the purpose of this analysis, we assume that the drug is administered as a continuous infusion so as to reach a steady‐state drug concentration. Thus, we can assume that the drug concentration C reaches its steady state faster as the PK half‐life is much shorter than the PD half‐life. This allows us to use a constant (nonzero) drug concentration in order to study the PD steady state in the presence of the drug. Thus, for a constant (nonzero) drug concentration .
From Eqs. (23) and (24), we conclude that at steady state we have:
| (25) |
Eliminating from the two equations in Eq. (25) yields:
| (26) |
which is a quadratic equation in variable v and has two solutions:
| (27) |
The two steady states are therefore:
| (28) |
where the former corresponds to the baseline steady state in the dimensional form. Note that the two steady‐state values of v are independent of the parameter (i.e., they are independent of the [constant] drug concentration), however, that is not the case for the u steady states.
Bifurcation
When a steady state x (which may be v 0 or v 1) depends on a parameter λ, then the graph of x vs. λ is called a “branch” of steady‐state solutions. When two branches intersect, one speaks of “bifurcation” and the point of intersection is called a “bifurcation point.” In Figure 7 b, we graph the solutions v 0 and v 1 against the parameter combination , under the assumption that γ = 1, so that . The graphs are straight lines that intersect at λ = 1, showing that the system undergoes a bifurcation as λ increases past one. The point of intersection is the bifurcation point.
Figure 7.
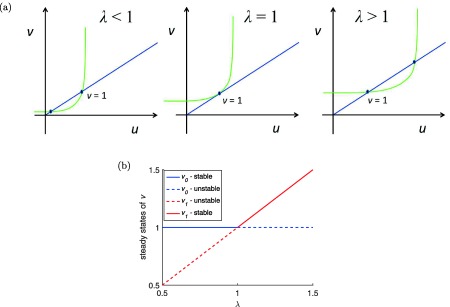
(a) Changes in the phase‐diagram as a function of the bifurcation ratio . Notice that for (the bifurcation point), the two steady states of v coalesce into just one steady state v = 1. (b) Bifurcation diagram showing the two steady states of plasma prolactin (PRL) concentration v and their stability as a function of the bifurcation parameter (MATLAB model code provided in Supplementary Figure S7).
Phase‐plane analysis
In this section, we present the phase‐plane analysis of the positive feedback model. We utilize this analysis in order to gain insight into the model behavior, specifically with respect to steady states, their stability, and bifurcation. Note that the analysis we present here applies to the case when the drug concentration C(t) is constant with time (i.e., ). Here, we consider the special case C = 0. The null clines are given by:
| (29) |
| (30) |
In Figure 6, we sketch the phase diagram for the positive feedback model for C = 0 (i.e., ). Note that Eq. (29) contains an Emax‐type function, so the corresponding null cline is a curve (rather than a straight line) similar to an Emax function.
Figure 6.
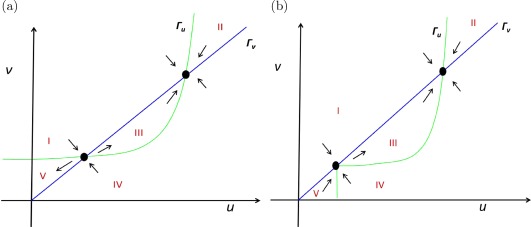
(a) Phase diagram of the nondimensionalized prolactin (PRL) pool model with positive feedback (Eqs. 23 and 24). Five regions I to V are identified and directions of vector fields in each region are sketched. The vector fields in the vicinity of the steady states are such that the lower steady state is unstable whereas the higher one is stable. (b) Phase diagram of the nondimensionalized PRL pool model with positive feedback including the “if condition” (Eqs. 31 and 32). Five regions I to V are identified and directions of vector fields in each region are sketched. The vector fields in the vicinity of the steady states are such that the lower steady state is stable from below whereas the higher one is globally stable.
Steady states
It can be seen that the two null clines intersect each other at two points (shown with black dots in the figure), which implies that the model has two steady states (except when λ = 1, when the two steady states merge).
Vector fields
The two null clines divide the phase‐plane in five distinct regions, identified as I to V (Figure 6 a). Vector fields are sketched in each region as in the sections above. These vector fields indicate the direction of orbits in each region (Figure 6 a).
Stability of steady states
Observing the vector fields close to the two steady states shows that the orbits behave differently in the vicinity of each steady state. It can be seen that all orbits seem to move toward the higher steady state. When all the orbits in the vicinity of a critical point (i.e., the steady state, in this case) converge toward the critical point as , such a critical point is called a “node.”
By inspecting the vector field closely one can prove that:
Orbits move SE (↘) and may exit through Γu to enter III or through Γv to enter IV or V, or converge to the steady state between III and V.
Orbits move SW (↙), cannot leave the region and converge to the steady state between IV and II.
Orbits move NE (↗), cannot leave the region and converge to the steady state between IV and II.
- Orbits from region IV move NW (↖) and can do the following:
- leave IV in finite time either through Γv to enter II or V, or through Γu to enter III.
- Stay in IV for all time and converge to either (u 0, v 0) (only one orbit) or to (u 1, v 1).
Orbits move SW (↙), cannot leave the region and leave the first quadrant.
Upper steady state
We conclude that all orbits in the vicinity of the upper steady state converge to this critical point as , so that this steady state is stable.
Lower steady state
Orbits starting in the vicinity of the lower steady state may enter region III and then converge to the upper steady state, or they may enter V and leave the first quadrant, or they may do neither and converge to the lower steady state (only one orbit does this). Evidently, this steady state is unstable and is called a “saddle point.”
REMARKS
Note that we have not used any values of the parameters (i.e., these stability properties are derived from the structure of the model itself).
Bifurcation and stability
We have shown that the model undergoes a bifurcation as the critical parameter λ increases past one. This is an example of a “transcritical bifurcation,” (i.e., a bifurcation point where the steady state [ ] moving along a branch that passes through it), that changes from stable to unstable or unstable to stable. We have seen that the upper steady state is the stable one. For that is v 0 and for it is v 1. Thus, as the parameter λ passes through the bifurcation point (λ = 1), stability is “exchanged” from v 0 to v 1. Figure 7 a shows geometrically how in the phase plane this transition takes place as λ passes from to and Figure 7 b shows the values of the two steady states and their stabilities as a function of the bifurcation parameter.
Physiologically desired steady state
The positive feedback model is a modified version of the original pool model, for which is the sole steady state. Thus, for the positive feedback model is the physiologically desired baseline plasma PRL concentration. This steady state is only stable when . Note that in the dimensional form the ratio . This parametric restriction can be implemented while data fitting is performed, so as to ensure that the expected steady state is stable.
Dynamics of the model without the “if condition”
When we use parameter values from ref. 12, we find that the bifurcation parameter is . This implies that the v 0, which corresponds to R 0, is the lower steady state and is unstable. The other steady state v 1 is stable (the value of this steady state in dimensional form is given as ng/mL).
Figure 8 a,b show the simulations of the positive feedback model given by Eqs. (23) and (24) for different doses D of risperidone: and 2 mg/kg (ref. 24 and Figure 5). The left panel shows graphs of v vs. t and the right panel shows orbits in the (u, v)‐plane. All orbits start from the lower baseline (1,1).
Figure 8.
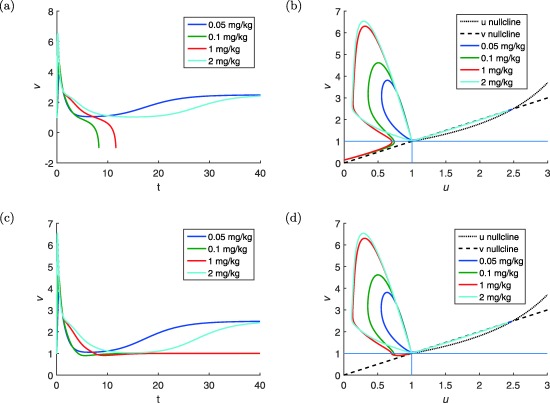
Simulations of the positive feedback model (Eqs. 23 and 24) without the if condition (a and b) and with the if condition (Eqs. 31 and 32) (c and d) for different doses D of risperidone: and 2 mg/kg. The drug pharmacokinetic (PK) is simulated using the PK model for s.c. dose of risperidone.24 (a and c) Dynamics of v vs. time. (b and d) Orbits of u and v plotted in the respective phase planes (MATLAB model code provided in Supplementary Figure S8).
Observations about the orbits in the phase plane
The orbits move into the NW direction (i.e., v increases and u decreases.) Moreover, they all leave the baseline in the same direction.
v reaches its maximum before u reaches its minimum.
For the larger doses, the orbits nearly coincide for a long time.
The orbits all return to a neighborhood of the baseline (1,1).
After the orbits have returned to the neighborhood of the baseline, there is a dichotomy:
-
(a)
Along two of the orbits (for doses 0.05 and 2 mg/kg) u and v continue to increase and these orbits eventually reach the higher steady state (u 1, v 1).
-
(b)
Two other orbits (for doses 0.1 and 1 mg/kg) take a turn and u and v begin to decrease. These orbits enter region V and leave the first quadrant. See Supplementary Material for the proof of why v becomes negative even though it denotes concentration.
DISCUSSION
The first observation can be understood from the fact that when we multiply Eq. (24) by α and add the resulting equation to Eq. (23), we obtain:
(i.e., in a neighborhood of the initial condition) the orbit is tangent to the line:
which is independent of the drug dose, and hence the same for each drug dose.
The second observation can be inferred from the two equations: when v reaches its maximum value, Eq. (24) states that , which, when used in the equation for , we see that for the given constants, so that the minimum of u is still to follow.
For larger doses, the orbits initially nearly coincide, because—as seen in Figure 8 b—for D = 1 and 2 mg/kg, C(t) ≫ SC50 = 0:08 for larger times, so that:
The dichotomy can now be understood as follows: the orbits return to a neighborhood of the baseline point (1,1). Because this is a saddle point, as is evident from the phase plane shown in Figure 6 a, small variations in the way the orbit approaches may have dramatic consequences for the way the orbit leaves the neighborhood: it may enter region V and leave the first quadrant, it may enter region III and move to the higher steady state v 1, or, in an exceptional case, it may approach v 0. However, it can be shown that there exists only one such orbit.
Dynamics of the model with the “if condition”
In the pool model with positive feedback section above, we presented the positive feedback model without an “if” condition (Eqs. (19) and (20)). The nondimensionalize version of the positive feedback model with the if condition is:
| (31) |
| (32) |
where the Heaviside function mathematically represents the if condition1 if and if v > 1. The null clines for the model with the if condition are:
| (33) |
or, alternatively:
| (34) |
| (35) |
| (36) |
Notice that for , the Γu does not depend upon v. Figure 6 b shows the phase plane for the model with if condition. The null clines divide the first quadrant in five disjoint regions (I to V), in which regions II, III, and IV are as in Figure 6 a, whereas the regions I and V are different.
Figure 8 c,d show the simulations of the model with the if condition given by Eqs. (31) and (32) for different doses D of risperidone: and 2 mg/kg (ref. 24 and Figure 5). Figure 5 c shows graphs of v vs. t and Figure 5 d shows orbits in the (u, v)‐plane. All orbits start from the lower baseline (1,1).
Observations about the orbits in the phase plane
Steps 1 to 4 are identical to those shown by the model without the “if condition.”
After the orbits have returned to the neighborhood of the baseline, there is a dichotomy in this model too:
Along two of the orbits (for doses 0.05 and 2 mg/kg) u and v continue to increase and these orbits eventually reach the higher steady state (u 1, v 1).
Two other orbits (for doses 0.1 and 1 mg/kg) take a turn and u and v begin to decrease. These orbits enter region V and of the phase plane (Figure 6 b) and continue onward to approach the lower steady state (1,1).
DISCUSSION
The initial movement of the orbits for the model with the “if condition” is the same as that for the model without the “if condition.” This is because the if condition does not affect the dynamics until an orbit reduces v below 1. At this point, the if condition is activated and effectively “switches off” the positive feedback. The resulting model is linear and has (1,1) as the only steady state (which is also stable). Thus, once an orbit enters region V of the phase plane in Figure 6 b, it can only proceed toward the lower steady state.
CONCLUSIONS
Through the mathematical analysis, so far we have tried to understand why the simulation of the positive feedback model with the if condition exhibits convergence to different steady states in an apparent dose‐dependent manner. Through steady‐state analysis we have learned that the nonlinearity in the model has resulted in multistationarity. Phase‐plane analysis has shown that the higher of the two steady states is always stable, whereas the lower steady state is stable from below. Furthermore, it has given a parametric condition under which the desired steady state can be (higher, and therefore,) always stable. For the parameters used by Stevens et al.,12 the desired steady state is the lower one, which is only stable from below. Simulating the model and plotting the orbits in the phase plane has shown that some orbits do not activate the if condition, and approach the higher steady state, whereas other orbits do activate the if condition and approach the lower steady state. This explains why the model exhibits convergence to two different steady states in response to different doses.
We noted in the dynamics of the model without the if condition section, that all the orbits move toward the vicinity of the lower steady state (and therefore on the border of activation of the if condition). Whether an orbit for certain doses does or does not activate the if condition would depend, not just upon the relative timescales of drug clearance, the PRL elimination rate, and PRL secretion rate, but also upon the accuracy of the numerical solver used. This sensitive behavior arises due to the characteristic vector field near the lower steady state and as such is very difficult to predict mathematically. Thus, even if one could use a fully accurate numerical solver, this unpredictable behavior would remain as it is a structural property of this model. This underlines the importance of using mathematical analysis to gain an insight into model behavior.
SUMMARY
In this tutorial, we have outlined the basic steps in dynamical systems analysis of ODE models. We have shown how the expressions for steady states can be obtained, how the stability of various steady states can be assessed, and how the parametric dependence of stability can be studied. We have also shown how phase planes can be very useful to gain knowledge about the dynamics of the system. We have illustrated all these steps with the help of the linear as well as a nonlinear variant of the pool model of PRL response. We have demonstrated how an apparently simple two ODE model can hide various interesting behaviors, which would be hard to uncover or understand through simulations alone. Three of the current authors also co‐authored the pool model with the PF article,12 however, the full scope of the model behavior remained unexplored at the time. Thus, simulations alone may not be relied upon and some insight into model behavior gained through such analytical techniques becomes crucial. Furthermore, such analyses could generate experimentally testable hypotheses to validate (or falsify) a model. Thus, modeling could inform pharmacological experimentation and vice versa.
We note that the techniques presented here are particularly well suited for analysis of small to medium size models. In particular, the phase‐plane analysis is suitable for 2‐ODE models. The 2‐ODE models may exhibit only a limited set of long‐time behaviors, namely asymptotic or oscillatory approach to steady states or sustained oscillations (not to mention lack of a steady state altogether). As we go from 2‐ODE to 3‐ODE models, the range of possible behaviors explodes and one can even expect chaotic behavior. Systems pharmacology models are expected to be larger and even more complex and their dynamical behaviors are likely to hide an even greater degree of complexity. However, as argued by Shankaran et al.,25 many large systems networks are formed of modules or motifs of small networks. Understanding the behavior of these small networks thoroughly using the techniques mentioned in this article can increase confidence in the understanding of the bigger networks.26, 27 At the same time, a few mathematical techniques, such as quasi‐steady state analysis and model reduction, informed by small parameter values may be useful to reduce the model size while retaining essential behavior. We hope that this tutorial not only equips the reader with a few techniques of mathematical analysis, but also highlights why and how mathematics may be useful for ODE‐based models in PK‐PD analysis.
Supporting information
Supporting Information 1
Supporting Information S3
Supporting Information S4
Supporting Information S5
Supporting Information S6
Supporting Information S7
Supporting Information S8
Supporting Information S9
Supporting Information S10
Supporting Information S11
Supporting Information S12
Supporting Information Table 1
Supporting Information Table 2
Supporting Information Table 3
Acknowledgments
This project was supported by the Dutch Top Institute Pharma (TIPharma) PK‐PD Platform 2.0. We also like to thank Drs. Johannes Proost and Amit Taneja for bringing to our notice the counterintuitive behavior of the PF model.
References
- 1. van der Graaf, P.H. & Benson, N. Systems pharmacology: bridging systems biology and pharmacokinetics‐pharmacodynamics (PKPD) in drug discovery and development. Pharm. Res. 28, 1460–1464 (2011). [DOI] [PubMed] [Google Scholar]
- 2. Gaspar, R. et al Towards a European strategy for medicines research (2014–2020): the EUFEPS position paper on Horizon 2020. Eur. J. Pharm. Sci. 47, 979–987 (2012). [DOI] [PubMed] [Google Scholar]
- 3. Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering. 2nd ed (Westview Press, Boulder, CO, 2014). [Google Scholar]
- 4. Kaplan, D. & Glass, L. Understanding Nonlinear Dynamics (Springer, New York, NY, 1995). [Google Scholar]
- 5. Murray, J.D. Mathematical Biology I: An Introduction (Springer, New York, NY, 2002). [Google Scholar]
- 6. Murray, J.D. Mathematical Biology II: Spatial Models and Biomedical Applications (Springer, New York, NY, 2003). [Google Scholar]
- 7. Ekblad, E.B. & Licko, V. A model eliciting transient responses. Am. J. Physiol. 246(1 Pt 2), R114–R121 (1984). [DOI] [PubMed] [Google Scholar]
- 8. Movin‐Osswald, G. & Hammarlund‐Udenaes, M. Prolactin release after remoxipride by an integrated pharmacokinetic‐pharmacodynamic model with intra‐ and interindividual aspects. J. Pharmacol. Exp. Ther. 274, 921–927 (1995). [PubMed] [Google Scholar]
- 9. Sharma, A. , Ebling, W.F. & Jusko, W.J. Precursor‐dependent indirect pharmacodynamic response model for tolerance and rebound phenomena. J. Pharm. Sci. 87, 1577–1584 (1998). [DOI] [PubMed] [Google Scholar]
- 10. Gabrielson, J. & Weiner, D. Pharmacokinetic and Pharmacodynamic Data Analysis: Concepts and Applications 4th ed (Swedish Pharmaceutical Press, Stockholm, Sweden, 2006). [Google Scholar]
- 11. Hazra, A. , Krzyzanski, W. & Jusko, W.J. Mathematical assessment of properties of precursor‐dependent indirect pharmacodynamic response models. J. Pharmacokinet. Pharmacodyn. 33, 683–717 (2006). [DOI] [PubMed] [Google Scholar]
- 12. Stevens, J. et al Mechanism‐based PK‐PD model for the prolactin biological system response following an acute dopamine inhibition challenge: quantitative extrapolation to humans. J. Pharmacokinet. Pharmacodyn. 39, 463–477 (2012). [DOI] [PubMed] [Google Scholar]
- 13. Zuideveld, K.P. et al A set‐point model with oscillatory behavior predicts the time course of 8‐OH‐DPAT‐induced hypothermia. Am. J. Physiol. Regul. Integr. Comp. Physiol. 281, R2059–R2071 (2001). [DOI] [PubMed] [Google Scholar]
- 14. Schmidt, S. , Post, T.M. , Peletier, L.A. , Boroujerdi, M.A. & Danhof, M. Coping with time scales in disease systems analysis: application to bone remodeling. J. Pharmacokinet. Pharmacodyn. 38, 873–900 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Segel, L.A. & Slemrod, M. The quasi‐steady‐state assumption: a case study in perturbation. SIAM Rev. 31, 446–477 (1989). [Google Scholar]
- 16. Peletier, L.A. , Benson, N. & van der Graaf, P.H. Impact of plasma‐protein binding on receptor occupancy: an analytical description. J. Theor. Biol. 256, 253–262 (2009). [DOI] [PubMed] [Google Scholar]
- 17. Bender, C.M. & Orzag, S.A. Advanced Mathematical Methods for Scientists and Engineers (Springer‐Verlag, New York, NY, 1999). [Google Scholar]
- 18. Gerlo, S. , Davis, J.R. , Mager, D.L. & Kooijman, R. Prolactin in man: a tale of two promoters. Bioessays 28, 1051–1055 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Petty, R.G. Prolactin and antipsychotic medications: mechanism of action. Schizophr. Res. 35Suppl, S67–S73 (1999). [DOI] [PubMed] [Google Scholar]
- 20. Movin‐Osswald, G. , Hammarlund‐Udenaes, M. , von Bahr, C. , Eneroth, P. & Walton‐Bowen, K. Influence of the dosing interval on prolactin release after remoxipride. Br. J. Clin. Pharmacol. 39, 503–510 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Ben‐Jonathan, N. , LaPensee, C.R. & LaPensee, E.W. What can we learn from rodents about prolactin in humans? Endocr. Rev. 29, 1–41 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Piccoletti, R. , Maroni, P. , Bendinelli, P. & Bernelli‐Zazzera, A. Rapid stimulation of mitogen‐activated protein kinase of rat liver by prolactin. Biochem. J. 303(Pt 2), 429–433 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Singh, M. , Sétáló, G. Jr , Guan, X. , Warren, M. & Toran‐Allerand, C.D. Estrogen‐induced activation of mitogen‐activated protein kinase in cerebral cortical explants: convergence of estrogen and neurotrophin signaling pathways. J. Neurosci. 19, 1179–1188 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Kozielska, M. et al Pharmacokinetic‐pharmacodynamic modeling of the D2 and 5‐HT (2A) receptor occupancy of risperidone and paliperidone in rats. Pharm. Res. 29, 1932–1948 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Shankaran, H. , Resat, H. & Wiley, H.S. Cell surface receptors for signal transduction and ligand transport: a design principles study. PLoS Comput. Biol. 3, e101 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Hartwell, L.H. , Hopfield, J.J. , Liebler, S. & Murray, A.W. From molecular to modular cell biology. Nature 402(6761 Suppl), C47–C52 (1999). [DOI] [PubMed] [Google Scholar]
- 27. Ma, W. , Lai, L. , Ouyang, Q. & Tang, C. Robustness and modular design of the drosophila segment polarity network. Mol. Syst. Biol. 2, 70 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information 1
Supporting Information S3
Supporting Information S4
Supporting Information S5
Supporting Information S6
Supporting Information S7
Supporting Information S8
Supporting Information S9
Supporting Information S10
Supporting Information S11
Supporting Information S12
Supporting Information Table 1
Supporting Information Table 2
Supporting Information Table 3


