Integrative analysis of genome-scale data by using pseudoinverse projection predicts novel correlation between DNA replication and RNA transcription

Abstract

We describe an integrative data-driven mathematical framework that formulates any number of genome-scale molecular biological data sets in terms of one chosen set of data samples, or of profiles extracted mathematically from data samples, designated the “basis” set. By using pseudoinverse projection, the molecular biological profiles of the data samples are least-squares-approximated as superpositions of the basis profiles. Reconstruction of the data in the basis simulates experimental observation of only the cellular states manifest in the data that correspond to those of the basis. Classification of the data samples according to their reconstruction in the basis, rather than their overall measured profiles, maps the cellular states of the data onto those of the basis and gives a global picture of the correlations and possibly also causal coordination of these two sets of states. We illustrate this framework with an integration of yeast genome-scale proteins' DNA-binding data with cell cycle mRNA expression time course data. Novel correlation between DNA replication initiation and RNA transcription during the yeast cell cycle, which might be due to a previously unknown mechanism of regulation, is predicted.

Recent advances in high-throughput technologies enable monitoring molecular biological signals, e.g., mRNA expression levels and proteins' DNA-binding occupancy levels, that correspond to activities of cellular systems, e.g., DNA replication, RNA transcription, and proteins' DNA-binding on a genomic scale. Integrative analysis of these global signals promises to give new insights into cellular mechanisms of regulation, i.e., global causal coordination of cellular activities. Integrative analysis of different types of large-scale molecular biological data requires mathematical tools that are able to formulate any number of large-scale data sets in terms of a common frame of reference, while reducing the complexity of the data to make them comprehensible (1, 2). These tools should provide data-driven models or mathematical frameworks for the description of the data, where the variables, i.e., the patterns that they uncover in the data, and operations, i.e., data reconstruction and classification in subspaces spanned by these patterns, may represent some biological reality.

Recently we showed that singular value decomposition (SVD) (3, 4) and generalized SVD (GSVD) (5) provide such data-driven frameworks for genome-scale molecular biological data. For example, the variables of SVD, “eigengenes” and corresponding “eigenarrays,” in the analyses of yeast Saccharomyces cerevisiae cell cycle time course mRNA expression data (6), and those of GSVD, “genelets” and corresponding “arraylets,” in the comparative analysis of yeast and human (7) cell cycle time course mRNA expression data, were shown to correlate with observed genome-scale effects of known cell cycle regulators and measured samples of the cell cycle stages that they regulate, respectively. Mathematical reconstruction of the yeast data in these subsets of eigengenes and corresponding eigenarrays, or genelets and corresponding arraylets, was shown to simulate approximately the experimental observation of the cell cycle progression alone, rather than the cell cycle progression together with concurrent biological processes and experimental artifacts. Mathematical classification of yeast genes and arrays according to their expression of these eigengenes and eigenarrays, or genelets and arraylets, rather than overall expression, mapped the data onto cell cycle stages and outlined the progression of the cell cycle along genes and in time, respectively.

Now we show that pseudoinverse projection (8) provides an integrative data-driven framework that formulates any number of genome-scale data sets in terms of a chosen set of data samples, or profiles extracted mathematically from data samples, which is designated the “basis” set. Pseudoinverse projection of a data set onto the basis set is a linear transformation of the data set from the open reading frames (ORFs) × data-samples space to the data-samples × basis-samples space, where each of the data samples is least-squares-approximated as a linear superposition of the basis profiles. We show that mathematical reconstruction of the data in the basis may simulate experimental observation of only the cellular states manifest in the data that correspond to those of the basis. Mathematical classification of the data samples according to their reconstruction in the basis, rather than their overall molecular biological profiles, maps the cellular states of the data onto those of the basis and gives a global picture of the correlations and possibly also coordination of these two sets of cellular states. Novel correlations between data samples and basis profiles might be due to previously unknown mechanisms of regulation.

We illustrate this framework with an integration of yeast genome-scale proteins' DNA-binding occupancy data (9) of nine cell cycle transcription factors (10) and four DNA replication initiation proteins (11) with the cell cycle time course mRNA expression data, using as basis sets the eigenarrays and arraylets determined by SVD and GSVD, respectively.¶

Mathematical Methods: Pseudoinverse Projection

Let the basis matrix b̂, of size N-ORFs or genomic sites × M-basis profiles, tabulate M genome-scale molecular biological profiles, measured from a set of M samples or extracted mathematically from a set of M or more measured samples. The vector in the nth row of the matrix b̂, 〈n|b̂, lists the signal of the nth ORF across the different samples which correspond to the different arrays.∥ The vector in the mth column of the matrix b̂, |b_m〉 ≡ b̂|m〉, lists the measured genome-scale signal levels of the mth basis sample. Let the data matrix d̂, of size N-ORFs × L-data samples, tabulate a genome-scale molecular biological data set of a different type of data and for the same ORFs in the same genome, measured in L samples. The vector in the lth column of the matrix d̂, |d_l〉 ≡ d̂|l〉, lists the measured genome-scale signal levels of the lth data sample.

Moore–Penrose pseudoinverse projection (8) of the data matrix d̂ onto the basis matrix b̂ is then a linear transformation of the data d̂ from the N-ORFs × L-data samples space to the M-basis profiles × L-data samples space (see Fig. 5 and Appendix, which are published as supporting information on the PNAS web site),

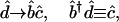[1]

where the matrix b̂^†, i.e., the pseudoinverse of b̂ satisfies

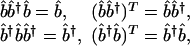[2]

such that the transformation matrices b̂b̂^† and b̂^†b̂ are orthogonal projection matrices. The pseudoinverse of b̂ is data-driven and unique. In this space the data matrix d̂ is represented by the matrix ĉ, which tabulates the correlations between the M vectors that span the pseudoinverse b̂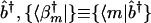^†, , and the L profiles of the samples that span the data matrix d̂, {|d_l〉}, such that 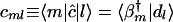for all 1 ≤ m ≤ M and 1 ≤ l ≤ L.

Pseudoinverse Computation. We use the SVD of the basis matrix b̂ = ûŵv̂^T, where ŵ is a diagonal nonnegative matrix, û^Tû = v̂^Tv̂ = Î, and Î is the identity matrix, to compute the pseudoinverse b̂^† = v̂ŵ^–1û^T, such that Eq. 2 is satisfied, and b̂b̂^† = ûû^T and b̂^†b̂ = v̂v̂^T are orthogonal projection matrices. We then compute the pseudoinverse correlations ĉ from b̂^† and d̂. We also compute the canonical correlation of each data profile with the basis, 0 ≤ 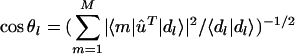≤ 1.

Integrative Data Reconstruction. The pseudoinverse projection of d̂ onto b̂ allows reconstruction of the data, d̂ → b̂b̂^†d̂, where each of the data samples is least-squares-approximated by a linear superposition of the basis profiles, 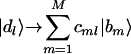, without eliminating ORFs or samples. For reconstruction and visualization, we set the arithmetic mean of each ORF across the samples and that of each sample across the ORFs to zero, such that each ORF and sample in the reconstructed data set is centered at its sample- or ORF-invariant level, respectively.

Integrative Data Classification. The reconstructed data samples are classified by similarity in the contributions of the basis profiles to their overall measured profiles rather than by their overall measured profiles alone.

Consider a basis that is determined by SVD analysis of a set of measured samples, and is spanned by M > 2 eigenarrays, {|b_m〉}, two of which, |b̂₁〉 and |b̂₂〉, span a subspace of interest. We plot the correlation of 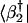with each reconstructed data sample |d_l〉, c_2l〈d_l|b̂b̂^†|d_l〉^–½, along the y-axis vs. that of 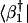along the x-axis. In this plot, the distance of each sample from the origin is its amplitude in the subspace spanned by |b₁〉 and |b₂〉 relative to its overall reconstructed amplitude, 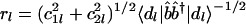. The angular distance of each sample from the x-axis is its phase in the transition from the profile |b₁〉 to |b₂〉 and back to |b₁〉, tan φ_l = c_2l/c_1l. We sort the reconstructed samples according to their angular distances from the x-axis, φ_l.

Consider also a basis that is determined by GSVD comparative analysis of two sets of measured samples and is spanned by M > 2 arraylets of one of these sets, {|b_m〉}. We approximate this basis with that spanned by the two vectors 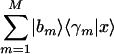and 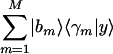, where the vectors |x〉 and |y〉 least-squares-approximate the corresponding M-genelets subspace, {〈γ_m|}, and maximize 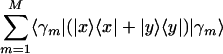. We plot the projection of each data sample, |d_l〉, from the M-arraylets subspace onto 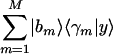, that is 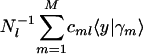along the y-axis vs. that onto along the x-axis, normalized by its ideal amplitude, where the contribution of each arraylet to the overall projected sample adds up rather than cancels out, 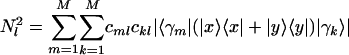. In this plot, the distance of each sample from the origin, r_l, is the amplitude of its normalized projection. An amplitude of 1 indicates that the contributions of the arraylets add up, and an amplitude of 0 indicates that they cancel out. The angular distance of each sample from the x-axis, φ_l, is its phase in the transition from the profile 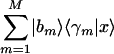to 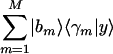and back, going through the projections of all M arraylets in this subspace. Again, we sort the reconstructed samples according to φ_l.

Independently, we also parallel- and antiparallel-associate each data sample with most likely parallel and antiparallel cellular states, or none thereof, according to the annotations of the two groups of n ORFs each, with largest and smallest levels of biological signal in this sample among all N ORFs, respectively. The P value of a given association by annotation is calculated by using combinatorics and assuming hypergeometric probability distribution of the K annotations among the N ORFs, and of the subset of k ⊆ K annotations among the subset of n ⊂ N ORFs, 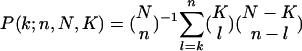, where 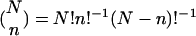is the binomial coefficient (12). We define the most likely association of a data sample with a cellular state as the association which corresponds to the smallest P value.

Biological Results: Integrative Analysis of mRNA Expression and Proteins' DNA-Binding Data

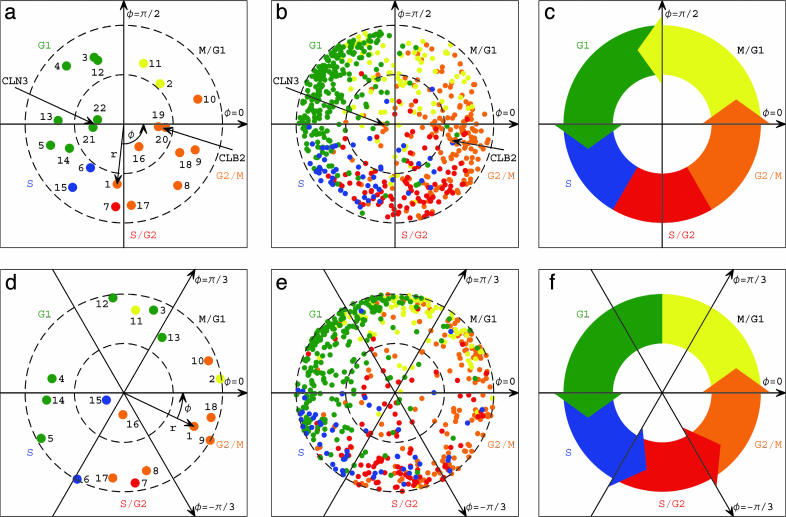
Basis Sets. (i) SVD cell cycle mRNA expression basis. SVD analysis (3, 4) of relative mRNA expression levels of 4,579 ORFs in 22 yeast samples measured by Spellman et al. (6) determined two dominant orthogonal eigenarrays and corresponding eigengenes of similar significance that span the yeast cell cycle expression subspace (see Data Sets 1 and 2 and Mathematica Notebook 1, which are published as supporting information on the PNAS web site). The 22 samples correspond to 18 samples of a cell cycle time course of an α-factor-synchronized culture, and two samples each of strains with overexpressed CLN3 and CLB2, which encode G₁ and G₂/M cyclins, respectively. One eigenarray was shown to correlate and anticorrelate with the samples of overexpressed CLN3 and CLB2, respectively (Fig. 1a). The corresponding eigengene was shown to correlate with CLN3 and its targets, i.e., genes for which expression peaks at the transition from G₁ to S, and anticorrelate with CLB2 and its respective targets, for which expression peaks at that from G₂/M to M/G₁ (Fig. 1b). Classification of the yeast arrays and genes in the subspaces spanned by these two eigenarrays and eigengenes gives a picture that resembles the traditional understanding of yeast cell cycle regulation (13): G₁ cyclins, such as Cln3, and G₂/M cyclins, such as Clb2, drive the cell cycle past either one of two antipodal checkpoints, from G₁ to S and from G₂/M to M/G₁, respectively (Fig. 1c). The SVD cell cycle mRNA expression basis we use is spanned by the M = 9 most significant eigenarrays across the N = 4,579 ORFs, including the two eigenarrays that span the SVD cell cycle expression subspace. (ii) GSVD cell cycle mRNA expression basis. GSVD comparative analysis (5) of mRNA expression of 4,523 yeast and 12,056 human ORFs in 18 samples each of time courses of α-factor-synchronized yeast culture (6), and double thymidine block-synchronized HeLa cell line culture measured by Whitfield et al. (7), determined six dominant genelets and corresponding six yeast and six human arraylets, at –π/3, 0 and π/3 initial phases, of similar significance in both data sets that span the yeast and human common cell cycle expression subspace (Data Sets 2, 3, and 4 and Mathematica Notebook 1, which are published as supporting information on the PNAS web site). The two 0-phase yeast arraylets were shown to correlate with cell cycle transition from G₂/M to M/G₁, in which the yeast culture is synchronized initially, and anticorrelate with that from G₁ to S (Fig. 1d). The two 0-phase human arraylets were shown to anticorrelate with the transition from G₂/M to M/G₁, and to correlate with that from G₁ to S, in which the human culture is synchronized initially. The two shared 0-phase genelets were shown to correlate with 0-phase oscillations of both yeast and human genes (Fig. 1e). Simultaneous classification of the yeast and human arrays and genes in the subspaces spanned by the six yeast and six human arraylets, and six shared genelets, respectively, gives a picture that resembles the traditional understanding of the biological similarity in the regulation of the yeast and human cell cycles (13), i.e., two antipodal checkpoints, at the transition from G₁ to S and at that from G₂/M to M/G₁, that are regulated independently of other cell cycle events (Fig. 1f). The GSVD cell cycle mRNA expression basis we use is spanned by the six yeast arraylets across the 4,523 ORFs.

Fig. 1.

The SVD (3, 4) and GSVD (5) cell cycle mRNA expression subspaces. (a) Normalized array correlation with the π/2-phase eigenarray along the y-axis vs. that with the 0-phase along the x-axis, color-coded according to the classification of the arrays into the five cell cycle stages by using combinatorics: M/G₁ (yellow), G₁ (green), S (blue), S/G₂ (red), and G₂/M (orange). The dashed unit and half-unit circles outline 100% and 25% of overall normalized array expression in this subspace. (b) Normalized correlation of each of the 646 cell cycle-regulated genes with the two corresponding eigengenes, color-coded according to either the traditional or microarray classifications. (c) The SVD picture of the yeast cell cycle. (d) Array expression, projected from the six-arraylets GSVD subspace onto π/2-phase along the y-axis vs. that onto 0-phase along the x-axis. The dashed unit and half-unit circles outline 100% and 50% of added up (rather than canceled out) contributions of the six arraylets to the overall projected expression. The arrows describe the projections of the –π/3-, 0-, and π/3-phase arraylets. (e) Expression of the 612 cell cycle-regulated genes, projected from the six-genelets GSVD subspace onto π/2-phase along the y-axis vs. that onto 0-phase along the x-axis. (f) The GSVD picture of the yeast cell cycle.

Data Sets. (i) Proteins' DNA-binding data. This data set tabulates the relative DNA-bound protein occupancy levels of the N = 2,928 ORFs with at least one valid data point in any one of L = 13 samples, which correspond to the nine yeast cell cycle transcription factors measured by Simon et al. (10) and four yeast replication initiation proteins measured by Wyrick et al. (11) (Data Set 5, which is published as supporting information on the PNAS web site). The relative binding occupancy level of the nth ORF in the lth sample is presumed valid when the P value calculated by either Simon et al. or Wyrick et al. that is associated with the measured relative binding occupancy signal is <0.1. We divide each ORF measurement by the arithmetic mean of the measurements for that ORF, thus converting the data to binding levels of each protein relative to those of all other proteins. (ii) α-Factor mRNA expression data. This set tabulates the relative mRNA expression levels of the 4,636 ORFs with valid data in all of the 18 samples of a cell cycle time course of an α-factor-synchronized culture (6) (Data Set 6, which is published as supporting information on the PNAS web site). The relative expression level of the nth ORF in the lth sample is presumed valid when the ratio of the measured expression signal to that of the background is >1 for both the synchronized culture and the asynchronous reference. (iii) CLB2 and CLN3 mRNA overexpression data. This set tabulates mRNA expression of 5,840 ORFs with valid data in four samples, two samples each of strains with overexpressed CLN3 and CLB2, which encode G₁ and G₂/M cyclins, respectively (6) (Data Set 7, which is published as supporting information on the PNAS web site). (iv) CDC15 mRNA expression data. This set tabulates mRNA expression of 4,122 ORFs with valid data in all 24 samples of a cell cycle time course of a yeast CDC15 mutant culture synchronized by temperature change (6) (Data Set 8, which is published as supporting information on the PNAS web site).

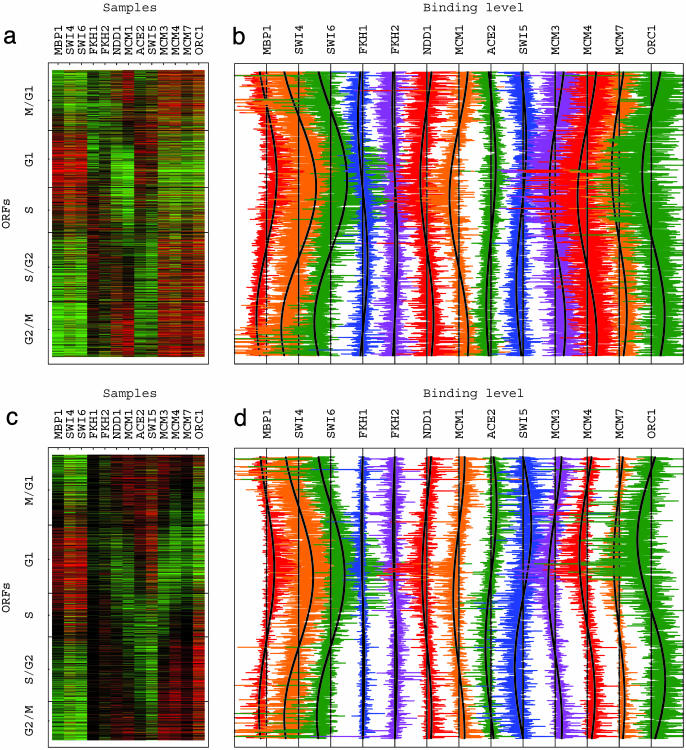
Pseudoinverse Reconstruction of the Proteins' DNA-Binding Data in the mRNA Expression Bases. Of the 2,227 and 2,139 ORFs in the intersections of the 2,928 ORFs of the proteins' DNA-binding data set and the 4,579 and 4,523 ORFs of the SVD- and GSVD-cell cycle mRNA expression bases, 400 and 377 ORFs were microarray-classified, and 58 and 60 were traditionally classified as cell cycle-regulated, respectively. In these intersections, at least one canonical correlation of each binding profile with either the SVD or GSVD bases is >0.1 (see Fig. 6 and Mathematica Notebook 2, which are published as supporting information on the PNAS web site). We reconstruct the proteins' DNA-binding data in the SVD and GSVD bases by using pseudoinverse projections in these intersections (Fig. 2). With the ORFs sorted according to their SVD and GSVD cell cycle phases, the ORF variations of the SVD- and GSVD-reconstructed binding profiles approximately fit cosine functions of one period and of varying initial phases. With the nine transcription factors ordered Mbp1, Swi4, Swi6, Fkh1, Fkh2, Ndd1, Mcm1, Ace2, and Swi5, following Simon et al. (10), the SVD- and GSVD-pseudoinverse correlations approximately fit cosine functions of one period and of varying initial phases across the nine samples, and are approximately invariant across the four samples of the replication initiation proteins, Mcm3, Mcm4, Mcm7, and Orc1 (Fig. 3).

Fig. 2.

Pseudoinverse reconstruction of the proteins' DNA-binding data in the SVD (a and b) and GSVD (c and d) cell cycle mRNA expression bases, with the ORFs sorted according to their SVD- and GSVD phases, respectively. Raster displays (a and c), with overexpression (red), no change in expression (black), and underexpression (green), and line-joined graphs (b and d) of the SVD- and GSVD-reconstructed 13 binding profiles along 2,227 and 2,139 ORFs, centered at their sample- and ORF-invariant levels, show a traveling wave in the nine transcription factors and a standing wave in the four replication initiation proteins.

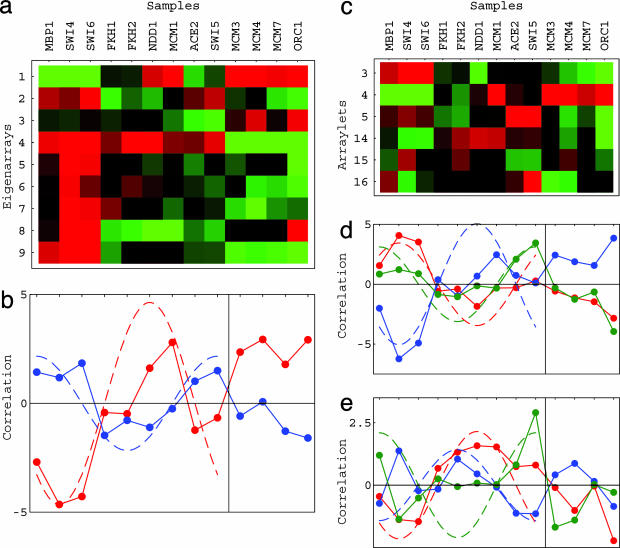
Fig. 3.

Pseudoinverse correlations of the proteins' DNA-binding data with the SVD (a and b) and GSVD (d and e) cell cycle mRNA expression bases. Shown are raster displays of ĉ ≡ b̂^†d̂, the correlations of the 13 binding profiles with the nine eigenarrays (a) and six arraylets (c) that span the SVD and GSVD bases, respectively. Also shown are line-joined graphs of the pseudoinverse correlations with the first (red) and second (blue) eigenarrays that span the SVD-cell cycle expression subspace (b), the third (red), fourth (blue), and fifth (green) arraylets (d), and the 14th (red), 15th (blue), and 16th (green) arraylets that span the GSVD cell cycle expression subspace (e).

The SVD- and GSVD-reconstructed transcription factors' data approximately fit traveling waves, cosinusoidally varying across the ORFs as well as the nine samples. Simon et al. (10) observed a similar traveling wave in the binding data of the nine transcription factors, ordered as above, across only 213 ORFs in the intersection of ORFs with a P value <0.001 for at least one data point in any one of the nine samples, and ORFs that were microarray-classified as cell cycle-regulated, sorted according to their cell cycle phases as calculated by Spellman et al. (6). These traveling waves are in agreement with current understanding of the cell cycle's progression of transcription along the genes and in time as it is regulated by DNA binding of the transcription factors at the promoter regions of the transcribed genes. Pseudoinverse reconstruction of the data in both the SVD and GSVD bases, therefore, simulates experimental observation of only proteins' DNA-binding cellular states that correspond to those of mRNA expression during the cell cycle. The SVD- and GSVD-reconstructed replication initiation proteins' data approximately fit standing waves, cosinusoidally varying across the ORFs and constant across the four samples, that are antiparallel to the reconstructed profiles of Mbp1, Swi4, and Swi6, and parallel to that of Mcm1.

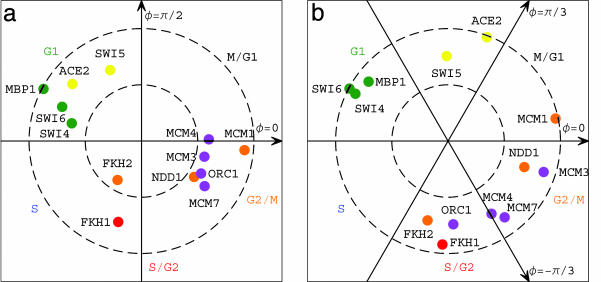
Pseudoinverse Mapping of the Proteins' DNA-Binding Data onto the Cell Cycle mRNA Expression Subspaces. We map the SVD- and GSVD-reconstructed proteins' DNA-binding data onto the SVD- and GSVD-cell cycle mRNA expression subspaces, respectively, associating with each binding profile cell cycle phase and amplitude (Fig. 4). Projected from the SVD basis, that is spanned by nine eigenarrays, onto the SVD-cell cycle subspace, which is spanned by two of these eigenarrays, all SVD-reconstructed samples have at least 25% of their binding profiles in this subspace, where their distances from the origin satisfy 0.5 ≤ r_l < 1, except for Fkh2. Projected from the six-dimensional GSVD-cell cycle subspace, which is spanned by six arraylets, onto the two-dimensional subspace that approximates it, 50% or more of the contributions of the six arraylets to each GSVD-reconstructed sample add up, where the distance of each array from the origin satisfies 0.5 ≤ r_l < 1.

Fig. 4.

Pseudoinverse mapping of the proteins' DNA-binding data onto the SVD (a) and GSVD (b) cell cycle mRNA expression subspaces. (a) Normalized sample correlation with the π/2-phase eigenarray along the y-axis vs. that with the 0-phase along the x-axis. (b) Sample binding projected from the six-arraylets GSVD subspace onto π/2-phase along the y-axis vs. that onto 0-phase along the x-axis.

Sorting the samples according to their SVD or GSVD phases gives an array order that is similar to that of Simon et al. (10) and describes the yeast cell cycle progression from the cellular state of Mbp1's binding through that of Swi5's. The SVD- and GSVD-mappings of the transcription factors' binding profiles onto the expression subspaces are also in agreement with the current understanding of the cell cycle program. Mapping the binding of Mbp1, Swi4, and Swi6 onto the cell cycle expression stage G₁ corresponds to the biological coordination between the binding of these factors to the promoter regions of ORFs and the subsequent peak in transcription of these ORFs during G₁. The mapping of Mbp1, Swi4, and Swi6 onto G₁, which is antipodal to G₂/M, also corresponds to their binding to promoter regions of ORFs that exhibit transcription minima or shutdown during G₂/M and to their minimal or lack of binding at promoter regions of ORFs that have transcription peaks in G₂/M. Similarly, the mapping of Mcm1 onto G₂/M corresponds to its binding to the promoter regions of ORFs that are subsequently transcribed during the transition from G₂/M to M/G₁. The binding profiles of the replication initiation proteins are SVD- and GSVD-mapped onto the cell cycle stage that is antipodal to G₁. This mapping is consistent with the reconstructed profiles of Mcm3, Mcm4, Mcm7, and Orc1 being antiparallel to those of Mbp1, Swi4, and Swi6 and parallel to that of Mcm1. Thus, DNA binding of Mcm3, Mcm4, Mcm7, and Orc1 adjacent to ORFs is shown to be correlated with minima or even shutdown of the transcription of these ORFs during the cell cycle stage G₁, suggesting a previously unknown genome-scale coordination between DNA replication initiation and RNA transcription during the cell cycle in yeast.

Independently, we also parallel- and antiparallel-associate each binding profile with most likely parallel and antiparallel cell cycle stages, or none thereof (Table 1, which is published as supporting information on the PNAS web site), by calculating the P value for the distribution of the 506 and 77 ORFs that were microarray and traditionally classified as cell cycle-regulated, respectively, among all 2,928 ORFs and among each of the subsets of 200 ORFs with largest and smallest levels of binding occupancy, respectively (Fig. 7, which is published as supporting information on the PNAS web site). At least one of the four P values for each profile, following either the microarray or traditional classification, for either parallel or antiparallel association, is <0.01. Most of the P values are «0.01. Almost all parallel and antiparallel associations of each profile are consistently antipodal, i.e., half of a cell-cycle period apart. Also, almost all associations following the microarray classification are consistent with the associations following the traditional classification. For example, following both the microarray and traditional classifications, the profile of Mcm1 is associated in parallel with G₂/M and in antiparallel with G₁. The SVD and GSVD mappings of all of the binding profiles onto the cell cycle transcription subspaces are consistent with these probabilistic associations by ORF annotations.

Pseudoinverse Integration of the mRNA Expression Data with the mRNA Expression Bases. We integrate the α-factor cell cycle, CLB2 and CLN3 overexpression and CDC15 cell cycle mRNA expression data sets with the SVD- and GSVD-cell cycle mRNA expression bases by using pseudoinverse projections (see Figs. 8–18 and Tables 2 and 3, which are published as supporting information on the PNAS web site). The results are all consistent and in agreement with the current understanding of the cell cycle program.

Pseudoinverse Integration of the Replication Initiation Proteins' DNA-Binding Data with the Transcription Factors' DNA-Binding Basis. We integrate the replication initiation proteins' DNA-binding data with the transcription factors' DNA-binding data after reconstruction in either the SVD- or GSVD-cell cycle RNA transcription bases (see Figs. 19 and 20, which are published as supporting information on the PNAS web site). Again we find that the binding profiles of the replication initiation proteins, Mcm3, Mcm4, Mcm7, and Orc1, are anticorrelated with the profiles of Mbp1, Swi4, and Swi6 and correlated with the profile of Mcm1.

Discussion

We showed that pseudoinverse projection can be used for integrative analysis of different types of large-scale molecular biological data. One consistent picture emerges upon integrating genome-scale proteins' DNA-binding data with the SVD- and GSVD-cell cycle mRNA expression bases, which is in agreement with the current understanding of the yeast cell cycle program. This picture correlates the binding of replication initiation proteins with minima or shutdown of the transcription of adjacent ORFs during the cell cycle stage G₁, under the assumption that the measured cell cycle mRNA expression levels are approximately proportional to cell cycle RNA transcription activity. It is known that replication initiation requires binding of Mcm3, Mcm4, Mcm7, and Orc1 at origins of replication across the yeast genome during G₁ (14, 15) and that these replication initiation proteins are involved with transcriptional silencing at the yeast mating loci (16, 17). It was suggested recently that the transcription factor Mcm1 also binds origins of replication (18). Either one of at least two mechanisms of regulation may be underlying this novel genome-scale correlation between DNA replication initiation and RNA transcription during the yeast cell cycle: The transcription of genes may reduce the binding efficiency of adjacent origins, or the binding of replication initiation proteins to origins of replication may repress, or even shut down, the transcription of adjacent genes. Thus a data-driven mathematical model, where the mathematical variables and operations represent biological reality, has been used to predict a biological principle that is truly on a genome-scale: The ORFs in either one of the basis or data sets were selected on the basis of data quality alone and were not limited to ORFs that are microarray or traditionally classified as cell cycle-regulated, suggesting that the RNA transcription signatures of yeast cell cycle cellular states may span the whole yeast genome. This idea is in agreement with the recent observation that a genome-wide oscillation in transcription gates DNA replication and the cell cycle (19).

Possible additional applications of pseudoinverse projection include integrating additional data of different cellular programs, e.g., yeast meiosis or invasive growth, and of different type, e.g., DNA sequence motif abundance in ORFs' promoter regions, DNA copy number, mRNA expression, or proteins' DNA-binding levels, with the basis set of yeast cell cycle mRNA expression to elucidate the coordination of these programs in terms of their genomic signals.