Unsupervised learning of natural languages

Abstract

We address the problem, fundamental to linguistics, bioinformatics, and certain other disciplines, of using corpora of raw symbolic sequential data to infer underlying rules that govern their production. Given a corpus of strings (such as text, transcribed speech, chromosome or protein sequence data, sheet music, etc.), our unsupervised algorithm recursively distills from it hierarchically structured patterns. The adios (automatic distillation of structure) algorithm relies on a statistical method for pattern extraction and on structured generalization, two processes that have been implicated in language acquisition. It has been evaluated on artificial context-free grammars with thousands of rules, on natural languages as diverse as English and Chinese, and on protein data correlating sequence with function. This unsupervised algorithm is capable of learning complex syntax, generating grammatical novel sentences, and proving useful in other fields that call for structure discovery from raw data, such as bioinformatics.

Many types of sequential symbolic data possess structure that is (i) hierarchical and (ii) context-sensitive. Natural-language text and transcribed speech are prime examples of such data: a corpus of language consists of sentences defined over a finite lexicon of symbols such as words. Linguists traditionally analyze the sentences into recursively structured phrasal constituents (1); at the same time, a distributional analysis of partially aligned sentential contexts (2) reveals in the lexicon clusters that are said to correspond to various syntactic categories (such as nouns or verbs). Such structure, however, is not limited to the natural languages; recurring motifs are found, on a level of description that is common to all life on earth, in the base sequences of DNA that constitute the genome. We introduce an unsupervised algorithm that discovers hierarchical structure in any sequence data, on the basis of the minimal assumption that the corpus at hand contains partially overlapping strings at multiple levels of organization. In the linguistic domain, our algorithm has been successfully tested both on artificial-grammar output and on natural-language corpora such as ATIS (3), CHILDES (4), and the Bible (5). In bioinformatics, the algorithm has been shown to extract from protein sequences syntactic structures that are highly correlated with the functional properties of these proteins.

The adios Algorithm for Grammar-Like Rule Induction

In a machine learning paradigm for grammar induction, a teacher produces a sequence of strings generated by a grammar G₀, and a learner uses the resulting corpus to construct a grammar G, aiming to approximate G₀ in some sense (6). Recent evidence suggests that natural language acquisition involves both statistical computation (e.g., in speech segmentation) and rule-like algebraic processes (e.g., in structured generalization) (7–11). Modern computational approaches to grammar induction integrate statistical and rule-based methods (12, 13). Statistical information that can be learned along with the rules may be Markov (14) or variable-order Markov (15) structure for finite state (16) grammars, in which case the EM algorithm can be used to maximize the likelihood of the observed data. Likewise, stochastic annotation for context-free grammars (CFGs) can be learned by using methods such as the Inside-Outside algorithm (14, 17).

We have developed a method that, like some of those just mentioned, combines statistics and rules: our algorithm, adios (for automatic distillation of structure) uses statistical information present in raw sequential data to identify significant segments and to distill rule-like regularities that support structured generalization. Unlike any of the previous approaches, however, adios brings together several crucial conceptual components; the structures it learns are (i) variable-order, (ii) hierarchically composed, (iii) context dependent, (iv) supported by a previously undescribed statistical significance criterion, and (v) dictated solely by the corpus at hand.

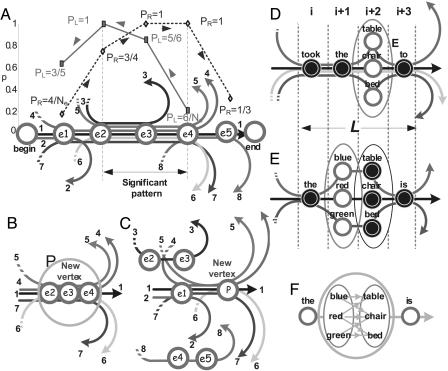
Consider a corpus of sentences (more generally, sequences) over a lexicon of size N, whose units in the case of language are words (starting with phonemes or letters, or even letters in a condensed text without spaces also works). The algorithm starts by loading the corpus onto a directed pseudograph (a nonsimple graph in which both loops and multiple edges are permitted) whose vertices are all lexicon entries, augmented by two special symbols, begin and end. Each corpus sentence defines a separate path over the graph, starting at begin and ending at end, and is indexed by the order of its appearance in the corpus. Loading is followed by an iterative search for significant patterns, which are added to the lexicon as new units. The structure of the data graph and the operations carried out on it are illustrated in Fig. 1. (See also Supporting Text, Figs. 4–17, and Tables 1–12, which are published as supporting information on the PNAS web site.)

Fig. 1.

The graph structures used by the MEX and adios algorithms. (A) The search path no. 1 (begin → e1 →... → e5 → end) is rendered as a solid black line connecting the special begin and end vertices. Four other paths (nos. 4, 5, 6, and 7) join it along the vertices e2, e3, e4, thus forming a bundle that may constitute a significant pattern subject to the MEX criterion described in BOX 1: The MEX Procedure. Values of P_R and P_L, originating at e1 and e4, respectively, are displayed for the example shown here. (B) A significant pattern (P = e2 → e3 → e4) has been identified. (C) A new vertex is added to the graph, replacing the elements subsumed by P. Paths that belong to sequences not subsumed by it, such as no. 3 here, are left untouched. (D) The path is generalized: the algorithm picks among the set of path segments encountered in a window of size L = 4 those that differ in a single slot and are embedded in a common context (the relevant vertices are marked by open circles). The vertices in this slot form an equivalence class E to be treated as a single unit, resulting in the first generalization step (see BOX 2: Theadios Algorithm). (E) The just-detected E(i + 2) is used to find an additional equivalence class; it is specific to the current common context, thus enhancing the safety of generalization. (F) Stacking two equivalence classes leads to further generalization (see BOX 2: The adios Algorithm for details).

The algorithm generates candidate patterns by traversing in each iteration a different search path (initially coinciding with one of the original corpus sentences), seeking subpaths that are shared by a significant number of partially aligned (2, 18) paths. The significant patterns (P) are selected according to a context-sensitive probabilistic criterion defined in terms of local flow quantities in the graph, stated in BOX 1: The Motif Extraction (MEX) Procedure. Generalizing the search path, the algorithm looks for an optional equivalence class (E) of units that are interchangeable in the given context [i.e., are in complementary distribution (2)]. At the end of each iteration, the most significant pattern is added to the lexicon as a new unit, the subpaths it subsumes are merged into a new vertex, and the graph is rewired accordingly (two rewiring modes are available: a context-free Mode A and a context-sensitive Mode B, as described in BOX 2: The adios Algorithm). The search for patterns and equivalence classes and their incorporation into the graph are repeated until no new significant patterns are found. The entire process is governed by the following three parameters: α and η, which control the definition of pattern significance, and L, which sets the width of the context window where equivalence classes are sought. We estimate the average-case computational complexity of the adios algorithm empirically to increase linearly with the size of the corpus (see section 7 of Supporting Text and Fig. 17).

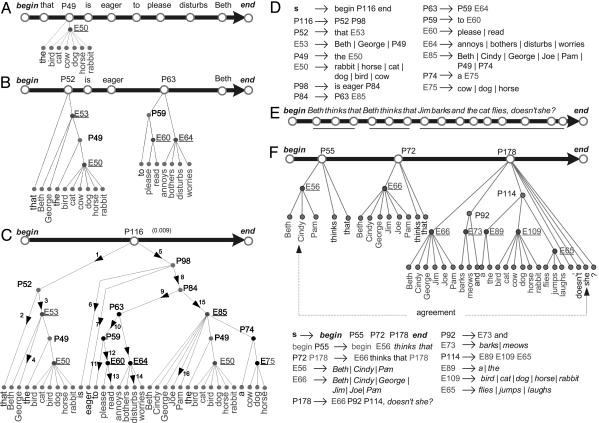
The final lexicon includes those of the original symbols not incorporated into larger units and a forest of tree-structured root patterns distilled by the algorithm (that is, the patterns that reside on the final graph, at the top level of the hierarchy). Each pattern is structured as a tree because of the hierarchical process of pattern creation; the leaves (terminals) are the original members of the lexicon, and the intermediate nodes are other patterns and equivalence classes (Fig. 2). The tree structure excludes cyclic recursion (loops) of patterns, although recursion may be introduced through pattern matching in a postprocessing stage.

Fig. 2.

Progressive abstraction of patterns constructs a forest of trees rooted in vertices of the graph (training data generated by a CFG, TA1; see Supporting Text). (A) Pattern P49, consisting of the terminal the and equivalence class E50 = {bird, cat, cow, dog, horse, rabbit}, is distilled. (B) Further application of the algorithm yields equivalence classes (underlined) such as E64, which contain some verbs. (C) Pattern P116 can generate 896 novel sentences, eight of which appear in the training corpus (the generalization factor, 8/896, appears in parentheses). A novel sentence, such as that George is eager to read disturbs Joe, can be read off the leaf level of the tree (numbered arrows indicate traversal order during generation). Pattern P116 is a root pattern, that is, a unit situated on a final path. (D) The set of context-free productions (rewriting rules) that is equivalent to the tree of pattern P116. (E) The initial path through a sentence to which adios was applied in the context-sensitive mode B. (F) The same path after three root patterns (P55, P72, and P178) have been distilled. Note how the two similar but not identical root patterns, P55 and P72, capture the difference between the equivalence classes E56 and E66 (indeed, Beth, for example, is equivalent to Jim in the context of P72 but not of P55). In this manner, adios enforces long-range agreement between E56 and the phrase doesn't she (embedded in P178) and avoids overgeneralization. (G) The two context-sensitive rules in this example are [begin P55 → begin E56 thinks that] and [P72 P178 → E66 thinks that P178].

The final graph includes as many paths as all of the original sentences, but it can also generate many new ones. To generate a sentence from a chosen path in the graph, all its root patterns are traversed. Each recursively encountered pattern is treated as a derivation or parse tree (19): it is read from top (root) to bottom (terminals) and from left to right, while accruing the terminals (words from the original lexicon) and selecting one member from each encountered equivalence class (Fig. 2C). Because the equivalence relations only hold in the contexts specified by their parent patterns, the adios representation is inherently safer than grammars that posit globally valid categories (such as “parts of speech” in a natural language). At the same time, because each rewiring of the graph brings closer far-apart units that used to straddle the newly abstracted pattern, the resulting representation can capture long-range structural dependencies among units.

Because patterns can be represented in the form of rewriting rules, which are context-free when Mode A is used (Fig. 2D) and context-sensitive when Mode B is used (Fig. 2G), the end product of an adios run constitutes a grammar. Because infinite recursion is not implemented in the current version of the algorithm, the representations learned by adios are comparable in expressive power to finite grammars that are at least context free. This means that any grammar consisting of context-free rules can be loaded into an adios instance (that is, translated into an adios representation), provided that a limit is placed on the number of times each rule is invoked recursively. In learning, the results described below show that our algorithm can acquire, from raw corpora, good operational approximations to those grammars that generate data rich with partially alignable sentences, including unconstrained natural-language data. Complex grammars that are inherently ambiguous (19) because of the presence of multiple loops are dealt with effectively by acquiring more patterns.

Results

To date, the adios algorithm has been tested on a variety of language data, as well as on DNA and protein sequences from several species. Details are available in Supporting Text.

Language: Computational Grammar Induction. In the domain of language, we tested the adios algorithm both on artificial-grammar data and on natural-language corpora such as ATIS (3) and CHILDES (4) and in languages as diverse as English and Chinese (5). It is reasonable to require that the success of a learning algorithm be measured by the closeness, ideally, identity, of the learned and target grammars, G and G₀, respectively. Unfortunately, even for CFGs, equivalence is undecidable (19). Moreover, for natural languages, G₀ is inaccessible. We thus opt for testing our implementation for generativity¶ as follows. In the artificial-grammar experiments, which start with a target grammar, a teacher instance of the model is first preloaded with this grammar (using the one-to-one translation of CFG rules into adios patterns), then used to generate the training corpus C_training. After training, the learner generates a test corpus C_learner and the teacher generates a test corpus C_target, the latter containing only novel sentences that do not appear in C_training. The two corpora, C_learner and C_target, then are used to calculate precision (the proportion of C_learner accepted by the teacher) and recall (the proportion of C_target accepted by the learner). A sentence is accepted if it precisely fits one of the paths in the adios graph (that is, it can be generated by the path). In the natural language experiments, where no target grammar is available, the given corpus is split into two portions, one for training (C_training) and one for testing (C_target), and the same evaluation method is applied, except that precision must in this case be evaluated by an external referee (e.g., by a human subject). This evaluation method is unique in that (i) it defines precision and recall more conservatively than is standard in the literature (21), and (ii) it involves testing both the capability of the learner to accept all of the grammatical sentences and its capability to generate only sentences that the teacher would deem grammatical.

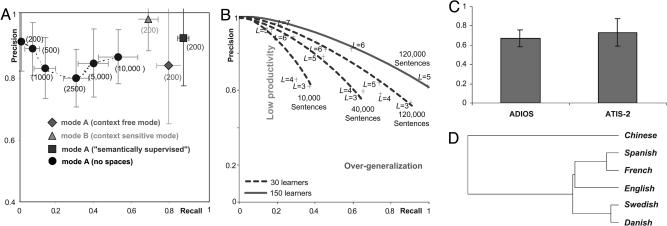
We have conducted a series of experiments designed to evaluate the performance of adios in grammar induction (Fig. 3). Learning a simple CFG. We first replicated an experiment (22) that aimed to reconstruct a specific CFG (29 terminals and 7 rules) from a corpus of 2,000 sentences. Whereas the algorithm proposed by ref. 22 generated between 3,000 and 4,000 rules, adios (used in the default Mode A) yielded 28 patterns and 9 equivalence classes and achieved 100% precision and 99% recall (see section 2.1 of Supporting Text and Table 1). Next, we applied adios to a somewhat more complex CFG (TA1 grammar, 50 terminals and 28 rules) and showed that it performs well even when only 200 sentences are used for training, as shown in Fig. 3A (see section 2.2 of Supporting Text, Tables 2–5, and Fig. 8). Learning a complex CFG. Because the adios algorithm is greedy (the best available pattern in each iteration is immediately and irreversibly rewired), the syntax it acquires depends on the order of sentences in the training set. This characteristic is expected to affect the learning of a complex CFG, especially if it contains many loops. To assess this dependence and to mitigate it, we train multiple learners on different order-permuted versions of the corpus generated by the teacher. As Fig. 3B illustrates, for the parameter values explored (L = {3,4,5,6}; 30 or 150 learners; corpus size between 10,000 and 120,000 sentences), the optimal precision-recall tradeoff for learning the ATIS CFG (357 terminals and 4,592 rules) [B. Moore and J. Carroll (2001), www.informatics.susx.ac.uk/research/nlp/carroll/cfg-resources] is obtained with a 150-learner cohort and L between 5 and 6 (see section 3.1 of Supporting Text, Table 7, and Fig. 9).

Fig. 3.

Experimental results. (A) The performance of an adios model trained on extremely small corpora generated by TA1. Optimal combinations of recall and precision (single learner, 30 trials, η = 0.6, α = 0.01, L = 5; maximum recursion depth for the teacher here and below set to 10) are shown for four different conditions as follows: (i) the default learning mode A (context-free mode, see BOX 2: The adios Algorithm); with a 800-sentence training corpus (data not shown), both precision and recall reach 90%; (ii) mode B (context-sensitive mode); (iii) a “semantically supervised” mode in which the equivalence classes of the target grammar are made available to the learner ahead of time [see evidence on the contribution of extra-linguistic knowledge to language acquisition (42)]; (iv) bootstrap mode, starting from a letter level and training on corpora in which all spaces between words are omitted. To maintain a comparable level of performance, the bootstrap mode requires larger corpora (size, shown in parentheses: 200–10,000 sentences). (B) Using the ATIS CFG (4,592 rules) (3) as the teacher of multiple adios learners. Precision is defined by the mean over learners, while for recall acceptance by one learner suffices. Several corpus sizes, context window widths L and numbers of learners are compared. (C) Output generated by an instance of adios that had been trained on the natural-language ATIS-2 corpus was judged to be as acceptable to human subjects as sentences from ATIS-2. Acceptability data (mean ± standard deviation) are from eight subjects. (D) A dendrogram illustrating the relationships among six different natural languages using pattern spectra. We define a pattern spectrum as the histogram of pattern types, whose bins are labeled by sequences such as (T, P) or (E, E, T) [E, equivalence class; T, tree-terminal (original unit); P, significant pattern]. This plot was generated by applying hierarchical clustering to a table of Euclidean distances among histograms of patterns learned by adios from online multilingual Bible texts (5), each consisting of ≈31,100 verses (single learner per language).

Generativity of the learned natural language grammar. To test the ability of adios to generate acceptable novel sentences after learning from a natural language corpus, we trained it on 12,700 sentences from the ATIS-2 natural language corpus of size 13,043 (3) and tested its recall level on the 343 remaining sentences. The small size of the training corpus results in a relatively low recall of 40% (under our strict definition that requires an exact match). Fig. 3C compares the acceptability of adios-generated sentences with original sentences from the ATIS-2 corpus (see section 4.1 of Supporting Text and Fig. 10). Notably, the output generated by adios is on the average as acceptable to human subjects as the original corpus sentences. The human-judged precision (≈70%, as shown in the plot) is remarkable; for comparison, the ATIS-CFG grammar, hand-constructed to fit the ATIS-2 corpus (with recall of 45% on same data) produces >99% ungrammatical sentences when used in a generative fashion.

Structural language modeling. A language model such as a table of word n-gram probabilities or a probabilistically annotated grammar can be made to predict the next word in a sentence from its predecessors, an operation that is highly useful in a variety of natural language processing tasks (23). A structured language model of the kind learned by adios, which includes reliable syntactic information, can be especially effective, because it captures longer-range dependencies than unstructured (purely statistical) n-gram models. When used as a language model on the ATIS-2 corpus (1,294-word lexicon; 11,386 unique sentences), adios achieved perplexity of 11.5 (see section 4.2 of Supporting Text and Fig. 11). ∥ In comparison, automatically acquired regular grammars achieve perplexity between 30 and 40; 3-gram models that use sophisticated smoothing of probabilities result in perplexity of ≈14 (24–27).

Languages other than English. Applying adios to the Parallel Bible (5) corpus, we compared six different languages through a metaanalysis of their respective adios grammars (see section 4.3 of Supporting Text and Fig. 12). The dendrogram shown in Fig. 3D captures the resulting typological relationships.

Bioinformatics. Although the present work focuses on language, adios also has been tested on various problems in bioinformatics; a representative result is reported here (another result is included in section 6.1 of Supporting Text, Tables 10 and 11, and Fig. 15A). We used the representations acquired by adios from protein sequence data to define a space where each protein is represented by a vector of its root-patterns. We then proceeded to show that this space supports functional classification of proteins, focusing on a family of enzymes whose functionality is captured by a homology tree structure of four levels. Classification of the 6,751 enzymes belonging to this family was tested previously by the svm-prot system (28), ** with the proteins described in terms of physical features (polarity, charge, etc.) of their building blocks. Despite using exclusively the raw sequence information, adios attained classification performance comparable with that of the svm-prot system (success rate of 95%). The same performance was attained also at the third level of the hierarchy. This result implies that the root-patterns extracted from raw sequence data carry useful functional information.

Discussion

The adios algorithm differs from other methods of grammar induction in the data it requires and the representations it builds, as well as in its algorithmic approach. Most existing methods require corpora tagged with part-of-speech information (29); the very few exceptions (30–22) are not known to scale up. The extraction of grammatical primitives in published methods may rely on collocation frequencies (30) or on global criteria such as the likelihood of the entire corpus given the grammar (14, 17, 29, 31, 32). In comparison, adios carries out its inferences locally, in the context provided by the current search path, alleviating the credit assignment problem in learning and making productive use of learned structures safer.

In its reliance on transition probabilities, the adios criterion for pattern significance may seem to resemble the well-known approaches that use various mutual information measures in defining syntactic constituents, such as the influential early work described in ref. 33. Mutual information-based approaches, however, are limited by diverse issues such as choosing the context window and alleviating the data sparseness problem (29), which our algorithm largely circumvents. In particular, when adios is iterated, symbols that may have been initially very far apart are allowed to exert influence on each other, enabling it to capture long-range syntactic dependencies such as agreement (Fig. 2F). Furthermore, adios works with raw text or transcribed speech, successfully overcoming the data sparseness problem through the use of a statistically feasible local-context significance criterion.

Although adios makes no prior assumptions about the structures it seeks, the patterns and equivalence classes it learns can be translated in a straightforward manner into the form of rewriting rules. These representations are both expressive enough to support extensive generativity, and, in principle, restrictive enough to capture many of the structure-sensitive aspects of syntax (1) documented by linguists, such as tough movement (see Fig. 8).

It is instructive to consider adios in the context of the problem of language acquisition, which has long been a daunting challenge for cognitive scientists (29, 34, 35). Because a completely bias-free unsupervised learning is impossible (34, 36), the real issue in language acquisition is to determine the model constraints. In our approach, the constraints are defined algorithmically in the form of a method for detecting units (patterns) that are hierarchically structured and supported by context-sensitive statistical evidence. When considered as a model of language acquisition, adios is clearly incomplete, because it currently relies on syntactic regularities and leaves out conceptual knowledge and grounding of speech acts in the external events. Nevertheless, our approach is compatible with a range of findings concerning language acquisition, such as the use of statistical cues (7, 37) and the importance of pattern-like constructions (38–40) (many more links to linguistic theories are offered in Supporting Text). Moreover, it performs well in a wide variety of situations that require unsupervised learning of structural information from untagged data. In grammar induction from large-scale raw corpora, our method achieves precision and recall performance unrivaled by any other unsupervised algorithm. It exhibits good performance in grammaticality judgment tests (including standard tests routinely taken by students of English as a second language) and replicates the behavior of human subjects in certain psycholinguistic tests of artificial language acquisition. Finally, the very same algorithmic approach also is proving effective in other settings where knowledge discovery from sequential data is called for, such as bioinformatics.

BOX 1: The Motif Extraction (MEX) Procedure

Seeking a Pattern Along a Search Path. The MEX procedure is applied for each search path of the adios graph that is to be explored for patterns. In the example of Fig. 1A, this is path no. 1: begin → e1 → ··· → e5 → end. Other paths may join and leave the search path at various vertices. In this example, the bundle of path sections between e2 and e4 display a certain coherence, possibly indicating the presence of a significant pattern.

Two probability functions are defined over the graph for any given search path. The first one, P_R, is the right-moving ratio of fan-through (through-going flux of paths) to fan-in (incoming flux of paths), which varies along the search path. Starting at e1 we define P_R at e2 as P_R(e1; e2) = (no. of paths from e1 to e2) divided by (total no. of paths entering e1).

At e3 it becomes P_R(e1; e3) = (no. of paths from e1 through e2to e3) divided by (total no. of paths from e1to e2). In Fig. 1 A, P_R first increases because other paths join to form a coherent bundle, then decreases at e5, because many paths leave the search path at e4. To quantify this decline of P_R, which we interpret as an indication of the end of the candidate pattern, we define a “decrease ratio,” D_R, whose value at e4 is D_R(e1; e4) = P_R(e1; e5)/P_R(e1; e4). We require that it be smaller than a preset “cutoff parameter” η < 1.

In a similar manner, we proceed leftward from some point down the search path (in the present example, starting at e4) and examine the left-going ratio of fan-through to fan-in, P_L. Thus, P_L(e4; e3) = (no. of paths from e3 to e4) divided by (total no. of paths entering e4) and so on. The value of P_L increases leftward; the point e2 at which it first shows a decrease D_L(e4; e2) = P_L(e4; e1)/P_L(e4; e2) < η is interpreted as the starting point of the candidate pattern.

The statistical significance of the decreases in P_R and P_L must be evaluated. P_R and P_L can be regarded as variable-order Markov probability functions. Continuing with the example of Fig. 1, we define their significance in terms of a null hypothesis stating that P_R(e1; e5) ≥ ηP_R(e1; e4) and P_L(e4; e1) ≥ ηP_L(e4; e2), and require that the P values of both D_R(e1; e4) < η and D_L(e4; e2) < η be, on average, smaller than a threshold α << 1.

A bundle of coinciding paths whose end-points obey these significance conditions is declared to be a candidate significant pattern. Given a search path, we calculate both P_L and P_R from all of the possible starting points (such as e1 and e4 in our example), traversing each path leftward and rightward, correspondingly. This technique defines many search-sections, which may be candidates for significant patterns. The most significant one of all these candidates is returned as the outcome pattern for the search path in question.

The Generalized Search Path. To generalize the notion of a search path, we consider a situation in which it contains an open slot where multiple alternative subpaths coexist within a fixed context defined by the main path. As an example, consider a window of size L = 3, composed of e2, e3, and e4, with a slot at e3. The generalized search path in this case consists of all of the paths that share the context e2,e4 and branch into all possible vertices at location e3. We thus define P(e₃|e₂; e₄) = Σ_β P(e_3β|e₂; e₄), where each P(e_3β|e₂; e₄) is calculated by considering a different path going through the corresponding e_3β. Likewise, we proceed to define P(e₅|e₂ e₃ e₄) = Σ_β P(e₅|e₂; e_3β; e₄) and so on. In the example of Fig. 1D, the generalized path is defined over a window of length 4 with one slot at the third location; the context at the other locations is fixed. In Fig. 1F, there are two slots, in locations 2 and 3.

BOX 2: The adios Algorithm

1. initialization: load all sentences as paths onto a pseudograph whose vertices are the unique words of the corpus.

2. pattern distillation: for each path (see Fig. 1 A–C for an illustration)

   1. find the leading significant pattern perform MEX on the search path by considering all search segments (i, j), j > i, starting P_R at e_i and P_L at e_j; choose out of all segments the leading significant pattern P for the search path.
   2. rewire graph create a new vertex corresponding to P.
      • Mode A (context free): replace the string of vertices comprising P with the new vertex P on all paths on which it occurs (Fig. 1C).
      • Mode B (context sensitive): replace the string of vertices comprising P with the new vertex P only on those paths on which P is significant according to the MEX criterion.

3. generalization–first step for each path (Fig. 1 D and E)

   1. slide a context window of size L along the search path from its beginning vertex to its end; at each step i (i = 1, ··· K – L – 1 for a path of length K) examine the generalized search paths: for all j = i + 1, ···, i + L – 2 do
      1. define a slot at location j;
      2. define the generalized path consisting of all paths that have identical prefix (at locations i to j – 1) and identical suffix (at locations j + 1 to i + L – 1);
      3. perform MEX on the generalized path;
   2. choose the leading P for all searches performed on each generalized path;
   3. for the leading P define an equivalence class E consisting of all the vertices that appeared in the relevant slot at location j of the generalized path;
   4. rewire graph create a new vertex corresponding to P (Fig. 1E) and replace the string of vertices it subsumes with the new vertex P on all paths where it occurs. We list here, and in the next rewiring step, only mode A; in mode B the replacement should occur only on the paths for which the new P is declared significant by MEX.

4. generalization–bootstrap for each path

   1. slide a context window of size L along the search path from its beginning vertex to its end; at each step i (i = 1, ··· K – L – 1 for a path of length K) do:
      construct generalized search path for all slots at locations j, j = i + 1, ···, i + L – 2, do
      1. consider all possible paths through these slots that start at vertex i and end at vertex K-L-1
      2. at each slot j compare the set of all encountered vertices to the list of existing equivalence classes, selecting the one E(j) that has the largest overlap with this set, provided it is larger than a minimum overlap ω (set to 0.65 in all our experiments);
   2. reduce generalized search path for each k, k = i + 1, ···, i + L – 2 and all j, j = i + 1, ···, i + L – 2 such that j ≠ k do
      1. consider the paths going through all the vertices in k that belong to E(j) [if no E(j) is assigned to a particular j, choose the vertex that appears on the original search-path at location j]; for all j (Fig. 1F);
      2. perform MEX on this reduced generalized path;
   3. extract the leading P; if the overlap of E(j) < 1 define a new equivalence class E′(j) containing only those members that did appear in the set;
   4. rewire graph create a new vertex corresponding to P (Fig. 1G) and replace the string of vertices subsumed by P with the new vertex P on all paths on which it occurs;

5. repeat step 4 (generalization) until no further significant patterns are found.