Understanding and comparisons of different sampling approaches for the Fourier Amplitudes Sensitivity Test (FAST)

Abstract

Fourier Amplitude Sensitivity Test (FAST) is one of the most popular uncertainty and sensitivity analysis techniques. It uses a periodic sampling approach and a Fourier transformation to decompose the variance of a model output into partial variances contributed by different model parameters. Until now, the FAST analysis is mainly confined to the estimation of partial variances contributed by the main effects of model parameters, but does not allow for those contributed by specific interactions among parameters. In this paper, we theoretically show that FAST analysis can be used to estimate partial variances contributed by both main effects and interaction effects of model parameters using different sampling approaches (i.e., traditional search-curve based sampling, simple random sampling and random balance design sampling). We also analytically calculate the potential errors and biases in the estimation of partial variances. Hypothesis tests are constructed to reduce the effect of sampling errors on the estimation of partial variances. Our results show that compared to simple random sampling and random balance design sampling, sensitivity indices (ratios of partial variances to variance of a specific model output) estimated by search-curve based sampling generally have higher precision but larger underestimations. Compared to simple random sampling, random balance design sampling generally provides higher estimation precision for partial variances contributed by the main effects of parameters. The theoretical derivation of partial variances contributed by higher-order interactions and the calculation of their corresponding estimation errors in different sampling schemes can help us better understand the FAST method and provide a fundamental basis for FAST applications and further improvements.

1. Introduction

Models are popular tools to help us understand and predict potential behaviors of different systems in physics, chemistry, biology, environmental sciences and social sciences. For a better use of the model and a better understanding of modeled systems, it is important that the model users quantify the overall amount of uncertainty in a model output (referred to as uncertainty analysis) and the importance of parameters in their contributions to uncertainty in the model output (referred to as sensitivity analysis). Sensitivity analysis techniques can be divided into two groups (Saltelli et al., 2000; Borgonovo et al., 2003): local sensitivity analysis methods and global sensitivity analysis methods. The local sensitivity analysis techniques examine the response of model output by varying model parameters one at a time around a local neighborhood of their central values. The global sensitivity techniques examine the global response (i.e., response averaged over variations of all parameters) of model output by exploring a finite (or even an infinite) region. The local sensitivity analysis is easy to implement, but dependent on central values of parameters. In addition, the local sensitivity analysis is not able to estimate the amount of uncertainty in the model output. Thus, global sensitivity analysis methods are generally preferred over local sensitivity analysis.

The global sensitivity analysis generally encompasses two processes: (1) sampling of parameters values from defined probability density functions for parameters; and (2) quantification of uncertainties in the model output contributed by different parameters. Many uncertainty and sensitivity analysis techniques are now available (Saltelli et al., 2000, 2005). They include Fourier Amplitude Sensitivity Test (FAST) (Cukier et al., 1973; Schaibly and Shuler, 1973; Cukier et al., 1975, 1978); the screening methods (Morris, 1991; Saltelli et al., 1995; Henderson-Sellers and Henderson-Sellers, 1996; Cryer and Havens, 1999; Beres and Hawkins, 2001; Saltelli et al., 2009); regression-based methods (Helton, 1993; Helton and Davis, 2002, 2003; Helton et al., 2005, 2006); Sobol's method (Sobol, 1993); McKay's one-way ANOVA method (McKay, 1997); and moment independent approaches (Park and Ahn, 1994; Chun et al., 2000; Borgonovo, 2006, 2007; Borgonovo and Tarantola, 2008). The global sensitivity analysis techniques differ in their algorithms for sampling or uncertainty quantifications.

FAST is one of the most popular global sensitivity analysis techniques. It uses a periodic sampling approach and a Fourier transformation to decompose the variance of a model output into partial variances contributed by different model parameters. Ratios of partial variances to model output variance are used to measure the parameters' importance in their contributions to uncertainty in the model output. The theory of FAST was first proposed by Cukier et al. (1973, 1975, 1978). The traditional FAST analysis uses a periodic sampling approach to generate a search curve in the parameter space. The periodic sample of each parameter is assigned with a characteristic frequency (i.e., a distinct integer), which is used to determine the parameter's contribution to the variance of a model output based on a Fourier transformation. Koda et al. (1979) and McRae et al. (1982) provided the computational codes for the traditional FAST analysis. To reduce the estimation errors in the sensitivity indices, characteristic frequencies need to be selected based on certain criteria (see Section 2.2 for details), which could be difficult for models with many parameters. In view of that, Tarantola et al. (2006) introduced a random balance design sampling method to avoid the difficulty of selecting characteristic frequencies. FAST analysis is originally developed for models with independent parameters. In order to extend FAST for models with dependent parameters, Xu and Gertner (2007, 2008) introduced a random reordering approach to account for rank correlations among parameters.

FAST is computationally efficient and can be used for nonlinear and non-monotonic models. Thus, it has been widely applied in the uncertainty and sensitivity analysis of different models, such as chemical reaction models (Haaker and Verheijen, 2004); atmospheric models (Collins and Avissar, 1994; Rodriguez-Camino and Avissar, 1998; Kioutsioukis et al., 2004); nuclear waste disposal models (Lu and Mohanty, 2001); soil erosion models (Wang et al., 2001); hydrological models (Francos et al., 2003); matrix population models (Xu and Gertner, 2009); and forest landscape models (Xu et al., 2009).

Although the FAST method has been widely applied to different models, it is mainly confined to the estimation of partial variances contributed by the main effects of model parameters. For the traditional search-curve based sampling, it has been heuristically shown for simple test models that FAST can be used to estimate partial variances contributed by parameter interactions using linear combination of characteristic frequencies through the exploration of Fourier amplitudes at different frequencies (Saltelli et al., 1999). Based on that, Saltelli et al. (1999) proposed a frequency selection method to estimate the sum of partial variances contributed by a special type of interactions (i.e., all interactions involving a parameter of interest) using the traditional search-curve based sampling. However, there is a lack of theoretical understanding and no proof for the calculation of partial variances contributed by the interactions among parameters, which may hinder future development of FAST. Furthermore the heuristic understanding does not allow for the estimation of partial variances contributed by the interactions among specific parameters due to a lack of knowledge of potential errors and biases for the estimation of partial variances. Finally, the heuristic understanding is only based on the traditional search-curve based sampling approach. It is important that we can also calculate the partial variances contributed by interactions for new sampling approaches (e.g., the random balance design sampling), in view that it would be difficult to apply the traditional sampling to modern models with many parameters (e.g., 50 parameters).

In this paper, we provide a theoretical derivation of FAST for higher-order sensitivity indices and compare three sampling approaches for FAST (i.e., traditional search-curve based sampling, simple random sampling, and random balance design sampling). We also analytically calculate the potential errors and biases in the estimation of partial variances with different sampling approaches. Finally, we compare the performance of the three sampling approaches for a simple test model. The theoretical derivation of partial variances contributed by higher order interactions and the calculation of their corresponding estimation errors in different sampling schemes can help us better understand the FAST method and extend FAST to applications where interactions among model parameters are concerned.

The paper is organized as follows. Section 2.1 introduces the background of FAST and provides a theoretical derivation of FAST for first-order and higher-order sensitivity indices. Section 2.2 provides algorithms for calculating partial variances contributed by the main effects and interaction effects of parameters for the traditional search-curve based sampling. Section 2.3 proposes a simple random sampling approach and hypothesis tests to reduce estimation errors and biases for partial variances. Section 2.4 introduces random balance design sampling and determines potential estimation errors and biases for partial variance calculations. Section 3 compares the estimation errors and biases in three sampling approaches and provides a summary of procedures for FAST analysis. Section 4 shows the results of a comparison of FAST using different sampling approaches based on a simple test model. Section 5 discusses extensions of the current framework for other potential improvements. Section 6 provides a summary of the paper.

2. Methods

2.1. Variance decomposition by FAST

Consider a computer model y = g(x₁,…, x_n), where x_i(i = 1,…, n) is a model parameter with probability density function f_i (x_i) and n is the total number of parameters of interest. The parameter space is defined as

$$K_x^n=\{x_1,\dots ,x_n|x_i\sim f_i(x_i),i=1,\dots ,n\}.$$ (1)

The original version of the FAST assumes independence among model parameters. The main idea of FAST is to introduce a signal for each parameter (by generating periodic samples of model parameters using a periodic sampling approach) and then use a Fourier transformation to decompose variance of model output y into partial variances contributed by different model parameters. In order to generate periodic samples for a specific parameter x_i, the FAST method uses a periodic search function (a function to search or explore the parameter space) as follows,

$$x_i=G({\theta }_i)=\stackrel{\sim }{G}(sin({\theta }_i))$$ (2)

where θ_i is a random variable uniformly distributed between 0 and 2π. For the sampled values of θ_i, the G(θ_i) is a periodic function used to generate the corresponding samples for parameter x_i which will follow the pre-specified probability density function f_i(x_i). For a uniformly distributed parameter x_i between 0 and 1, G̃ (x_i) should be a solution of the following equation (Cukier et al., 1978),

$$\pi \sqrt{1-x_i^2}\frac{\mathrm{d}\stackrel{\sim }{G}(x_i)}{\mathrm{d}{x}_i}=1$$ (3)

with G(0) = 0. Using the solution of Eq. (3), Saltelli et al. (1999) proposed one popular periodic search function as follows,

$$x_i=G({\theta }_i)=\frac{1}{2}+\frac{1}{\pi }arcsin(sin({\theta }_i)).$$ (4)

For a non-uniformly distributed function, the periodic search function can be built using the parameter's inverse cumulative distribution function $(\text{ICDF}:F_i^{-1}(\cdot ))$ and the search function in Eq. (4) becomes (Lu and Mohanty, 2001),

$$x_i=G({\theta }_i)=F_i^{-1}\left(\frac{1}{2}+arcsin(sin({\theta }_i))\right).$$ (5)

Using search functions based on Eq. (5), the parameter space can now be explored by samples in the θ-space defined as follows,

$$k_{\theta }^n=\{{\theta }_1,\dots ,{\theta }_n|0<{\theta }_i<2\pi ,i=1,\dots ,n\}.$$

A main concern in uncertainty and sensitivity analysis is to calculate the variance of model output y [i.e., V (y)] and the conditional variance of y the expected value of y given a specific set of parameters (Saltelli and Tarantola, 2002; Saltelli et al., 2010). The conditional variances are used to measure the importance of parameters in their contributions to uncertainty in the model output. For example, a relatively large conditional variance for the expected value of y given x_i [i.e., V(E(y | x_i))] will indicate that a relatively large proportion of model output variance is contributed by parameter x_i. Similarly, a relatively large conditional variance of the expected value of y given a specific set of parameters will indicate that a relatively large proportion of model output variance is contributed by this set of parameters. Using the Strong Law of Large Numbers, it can be shown that the conditional variances for the expected values of y given specific parameters can now be calculated in the θ-space (see Appendix A in supplementary materials for a proof). Namely,

$$\begin{array}{l}{V}^{(x_i)}=V_x(E_x(y|x_i))=V_{\theta }(E_{\theta }(y|{\theta }_i))\hfill \\ V^{(x_i,x_j)}=V_x(E_x(y|x_i,x_j))=V_{\theta }(E_{\theta }(y|{\theta }_i,{\theta }_j)),i\ne j\hfill \\ \dots \hfill \\ V^{(\{x_1,\dots ,x_n\}\backslash x_i)}=V_x(E_x(y|\{x_1,\dots ,x_n\}\backslash x_i))=V_{\theta }(E_{\theta }(y|\{{\theta }_1,\dots ,{\theta }_n\}\backslash {\theta }_i))\hfill \end{array}$$ (6)

where V_x(•) and are V_θ (•) the conditional variances calculated in the parameter space and θ-space respectively; E_x(•) and E_θ (•) are the expected values calculated in the parameter space and θ-space respectively; {x₁,…, x_n} \ x_i represents all parameters except x_i. For a subset (x_sub) of all parameters {x₁,…, x_n}, V^(x_sub) represents partial variance in model output y resulted from uncertainties in the subset parameters x_sub. V^{(x₁,…,x_n)} represents the variance of model output y resulted from uncertainties in all model parameters. Namely,

$$V^{(x_1,\dots ,x_n)}=V(y).$$ (7)

Following the variance decomposition in analysis of variance (ANOVA) assuming parameter independence (Saltelli and Tarantola, 2002), we define

$$\begin{array}{l}{V}_{x_i}=V^{(x_i)},\\ V_{x_i{x}_j}=V^{(x_i,x_j)}-V_{x_i}-V_{x_j},i\ne j\\ \dots \\ v_{x_1,\dots ,x_n}=v^{(x_1,\dots ,x_n)}-{\displaystyle \sum _{s=1}^r{\displaystyle \sum _{1\le i_1<i_2<\dots <i_s\le n}{v}_{x_{i_1},\dots ,x_{i_s}},r=1,2,\dots ,n-1}}\end{array}$$ (8)

as partial variances of model output contributed by the first-order (or main) effects, the second-order interaction effects, and so on, until the nth order interaction effects of model parameters. Summing all the left and right terms in Eq. (8), we get the variance decomposition as follows,

$$V^{(x_1,\dots ,x_n)}={\displaystyle \sum _{i=1}^n{V}_{x_i}}+{\displaystyle \sum _{i<j}{V}_{x_i{x}_j}}+{\displaystyle \sum _{i<j<K}{V}_{x_i{x}_j{x}_k}}+\dots +V_{x_1,\dots ,x_n}.$$ (9)

This equation suggests that the model output variance resulting from parameter uncertainties can be decomposed into partial variances contributed by the first-order effects, the second-order interaction effects, the third-order interaction effects, and so on, until the nth order interaction effects of model parameters. Dividing both sides of Eq. (9) by V^{(x₁,…,x_n)}, we get

$$1={\displaystyle \sum _{i=1}^n{\alpha }_{x_i}}+{\displaystyle \sum _{i<j}{\alpha }_{x_i{x}_j}}+{\displaystyle \sum _{i<j<k}{\alpha }_{x_i{x}_j{x}_k}}+\dots +{\alpha }_{x_1,\dots ,x_n}$$ (10)

where

$$\begin{array}{l}{\alpha }_{x_i}=\frac{V_{x_i}}{V^{(x_1,\dots ,x_n)}}\hfill \\ {\alpha }_{x_i,x_j}=\frac{V_{x_i,x_j}}{V^{(x_1,\dots ,x_n)}}\hfill \\ \dots \hfill \\ {\alpha }_{x_1,\dots ,x_n}=\frac{V_{x_1,\dots ,x_n}}{V^{(x_1,\dots ,x_n)}}\hfill \end{array}$$ (11)

represent the first, second, and so on until nth order sensitivity index, respectively.

Using search functions in Eq. (5), the model output y becomes a multiple periodic function of (θ₁,…, θ_n). Thus, we can apply a multiple Fourier transformation to the model y = g(G(θ₁),…, G(θ_n)) over (θ₁,…, θ_n). Namely, we have

$$g(G({\theta }_1),\dots ,G({\theta }_n))=\sum _{r_1,\dots ,r_n=-\infty }^{+\infty }{C}_{r_1,\dots ,r_n}^{(\theta )}{\mathrm{e}}^{\mathbf{i}(r_1{\theta }_1+\dots +r_n{\theta }_n)}$$ (12)

where

$$C_{r_1,\dots ,r_n}^{(\theta )}={\left(\frac{1}{2\pi }\right)}^n{\int }_0^{2\pi }\dots {\int }_0^{2\pi }g(G({\theta }_1),\dots ,G({\theta }_n)){\mathrm{e}}^{-\mathbf{i}(r_1{\theta }_1+\dots +r_n{\theta }_n)}\mathrm{d}{\theta }_1,\dots ,\mathrm{d}{\theta }_n.$$ (13)

Notice that $C_{r_1,\dots ,r_n}^{(\theta )}$ is the expected value of g(G(θ₁),…, G(θ_n))e^{−i(r₁θ₁+⋯+r_nθ_n)} in view that θ₁,…, θ_n are independently and uniformly distributed in the θ-space. Namely,

$${\widehat{C}}_{r_1,\dots ,r_n}^{(\theta )}=E_{\theta }(g(G({\theta }_1),\dots ,G({\theta }_n)){\mathrm{e}}^{-\mathbf{i}(r_1{\theta }_1+\dots +r_n{\theta }_n)})$$ (14)

which can be estimated based on N samples of θ₁,…, θ_n as follows,

$$C_{r_1,\dots ,r_n}^{(\theta )}=\frac{1}{N}\sum _{j=1}^N(g(G({\theta }_1^{(j)}),\dots ,G({\theta }_n^{(j)})){\mathrm{e}}^{-\mathbf{i}(r_1{\theta }_1^{(j)}+\dots +r_n{\theta }_n^{(j)})})$$ (15)

where ${\theta }_i^{(j)}$ represents the jth sample for θ_i· Using the multiple Fourier transformation, we can also estimate the partial variances in Eq. (8) by the sum of Fourier amplitudes (i.e., |C_r1,…,rn|²) at different frequencies (see Appendix B in supplementary materials for proof),

$$\begin{array}{l}{V}_{x_i}={\displaystyle \sum _{|r_i|=1}^{+\infty }|C_{00\dots r_i\dots 00}^{(\theta )}{|}^2}\\ V_{x_i{x}_j}={\displaystyle \sum _{|r_i|,|r_j|=1}^{+\infty }|C_{00\dots r_i\dots r_j\dots 00}^{(\theta )}{|}^2}\\ \dots \\ V_{x_1,\dots ,x_n}={\displaystyle \sum _{|r_1|,\dots ,|r_n|=1}^{+\infty }|C_{r_1\dots r_n}^{(\theta )}{|}^2},\end{array}$$ (16)

where r_i ∈ (−∞,+∞) for i = 1,…, n. Eq. (16) shows that the Fourier amplitudes $|C_{00\dots r_i\dots 00}^{(\theta )}{|}^2,|C_{00\dots r_i\dots r_j\dots 00}^{(\theta )}{|}^2$, and $|C_{r_1\dots r_n}^{(\theta )}{|}^2$ are resulted from the main effects, second order interaction effects, and nth interaction effects of parameters, respectively. Thus, to calculate the partial variances, we only need to estimate the Fourier coefficients based on Eq. (15). Summing all the terms in Eq. (16) based on Eq. (9), it is easy to show that

$$V(y)=V^{(x_1,\dots ,x_n)}=\sum _{|r_1|,\dots ,|r_n|=1}^{+\infty }|C_{r_1\dots r_n}^{(\theta )}{|}^2.$$ (17)

We need to point out that Cukier et al. (1978) have provided the same variance decomposition as we do in Eq. (17). They showed that the first-order Fourier amplitudes in Eq. (17) (i.e., $|C_{00\dots r_i\dots 00}^{(\theta )}{|}^2,r_i\ne 0$) are linked to the main effects of parameters and suggested that the higher-order Fourier amplitudes (e.g., $|C_{00\dots r_i\dots r_j\dots 00}^{(\theta )}{|}^2$ and $|C_{00\dots r_i\dots r_j\dots r_k\dots 00}^{(\theta )}{|}^2,r_i,r_j,r_k\ne 0$) may contain increasingly more detailed information about the coupling of sensitivity among larger groups of parameters. However, they did not provide a proof of the linkage between the higher-order Fourier amplitudes and higher-order interactions among parameters as shown in Eq. (16). Our derivation of this linkage (see Appendix B in supplementary materials) is based on the relationships between conditional variances in the parameter space and those in the θ-space [see Eq. (6)].

Notice that there is only one period for the sampled parameter values using the search functions in Eq. (5). Thus, there are strong signals for parameters in the Fourier amplitudes (i.e., $|C_{r_1\dots r_n}^{(\theta )}{|}^2$) when the fundamental frequency is equal to one (i.e., r₁ = 1, or r₂ = 1, …, or r_n = 1). The signals decrease at higher harmonics, which are integer multiples (termed the harmonic orders) of the fundamental frequency (Cukier et al., 1978). Signals in the Fourier amplitudes become close to zero, if any of r₁,…, r_n is relatively large (i.e., at a high harmonic order). The harmonic order at which the Fourier amplitudes become close to zero is defined as a maximum harmonic order (M), which is commonly four or six in practice, and could be larger for highly nonlinear models (Xu and Gertner, 2008).

2.2. Sampling based on an auxiliary variable

One intuitive approach to sample in the θ-space is the grid sampling, based on which we can numerically estimate the Fourier coefficients C_r1…rn using Eq. (15). However, the grid sampling can be very computationally expensive especially if there are many parameters. For example, a model with 10 parameters will need N¹⁰ samples, where N is the grid sample size for an individual parameter. Cukier et al. (1973) proposed a simple sampling approach by using a search curve in the θ-space with a common auxiliary variable (s). Namely,

$$\begin{array}{l}{\theta }_1=\phi ({\omega }_{1}s)={\omega }_{1}s\text{mod}2\pi \hfill \\ {\theta }_2=\phi ({\omega }_{2}s)={\omega }_{2}s\text{mod}2\pi \hfill \\ \dots \hfill \\ {\theta }_n=\phi ({\omega }_{n}s)={\omega }_{n}s\text{mod}2\pi \hfill \end{array}$$ (18)

where ω_i is a distinct integer frequency (or, a characteristic frequency) for parameter x_i and s ∈ [0, 2π] is a common auxiliary variable. For the auxiliary variable s, we can generate grid samples

$$\left\{s^{(1)},\dots ,s^{(N)}|s^{(j)}=\frac{\pi }{N}+\frac{2\pi }{N}(j-1),j=1,\dots ,N\right\},$$ (19)

based on which we can draw samples in the θ-space using a search curve with Eq. (18). Cukier et al. (1978) pointed out that if we select the characteristic frequencies in Eq. (18) to be free of interferences to an order M (M is generally four) (Cukier et al., 1975),

$$\sum _{i=1}^n{r}_i{\omega }_i\ne 0;r_i=\text{integer and}\sum _{i=1}^n|r_i|\le M+1,$$ (20)

then the search curve of Eq. (18) can effectively explore the θ-space. For a theoretical discussion in this paper, we define a frequency set {ω₁,…, ω_n} to be strictly free of interferences to an order M, if

$$\sum _{i=1}^n{r}_i{\omega }_i\ne 0;r_i=\text{integer and}|r_i|\le M.$$ (21)

Notice that the definition for frequencies strictly free of interferences to an order of M in Eq. (21) has more constraints on the frequency set than the definition for frequencies free of interferences in Eq. (20). For example, if we have 3ω₁ = 2ω₂ − ω₃ for {ω₁ = 3, ω₂ = 7, ω₃ = 5}, then there are interferences for M = 3 based on the definition in Eq. (21) but no interferences based on Eq. (20).

Based on the search curve of Eqs. (18) and (5), the model g(G(φ(ω₁s)),…, g(G(φ(ω_ns)))) becomes a periodic function of the auxiliary variable s. Therefore, we can also apply a Fourier transformation for g (G(φ (ω₁s)),…, G(φ (ω_ns))) over the auxiliary variable s. Namely,

$$g(G(\phi ({\omega }_{1}s)),\dots ,G(\phi ({\omega }_{n}s)))=\sum _{k=-\infty }^{+\infty }{C}_k^{(s)}{\mathrm{e}}^{\mathbf{i}(ks)}$$ (22)

Where

$$C_k^{(s)}=\frac{1}{2\pi }{\int }_0^{2\pi }g(G(\phi ({\omega }_{1}s)),\dots ,G(\phi ({\omega }_{n}s))){\mathrm{e}}^{\mathbf{i}(ks)}\mathrm{d}s.$$ (23)

Based on Parseval's theorem, variance of g(G(φ(ω₁s)),…, G(φ (ω_ns))) can be decomposed over integer frequencies as follows (Cukier et al., 1978),

$$V_s(g(G(\phi ({\omega }_{1}s)),\dots ,G(\phi ({\omega }_{n}s))))=\sum _{|k|=1}^{+\infty }|C_k^{(s)}{|}^2.$$ (24)

Eq. (23) indicates that C_k is the expected value of g(G(φ(ω₁s)),…, G(φ(ω_ns)))e^−i(ks) given s is uniformly distributed in (0, 2π). Namely,

$$C_k^{(s)}=E(g(G(\phi ({\omega }_{1}s)),\dots ,G(\phi ({\omega }_{n}s))){\mathrm{e}}^{-\mathbf{i}(ks)}).$$ (25)

Thus, the Fourier coefficient $C_k^{(s)}$ can be estimated based on the sample mean using a sample of size N,

$${\widehat{C}}_k^{(s)}=\frac{1}{N}\sum _{j=1}^{N}g(G(\phi ({\omega }_1{s}^{(j)})),\dots ,G(\phi ({\omega }_n{s}^{(j)}))){\mathrm{e}}^{-\mathbf{i}(k{s}^{(j)})}$$ (26)

where s^(j) is the jth sample for the auxiliary variable s. For a grid sample based on Eq. (19), the sample mean in Eq. (26) is essentially a numerical integral using the rectangle rule with a rectangle width of $\frac{2\pi }{N}$ (See Appendix C in supplementary material for details). With an increasing sample size of N, the estimation error decays at a rate of the square width of the rectangles, or at a rate of $\frac{1}{N^2}.$

For a frequency set {ω₁,…, ω_n}, the Fourier coefficient over auxiliary variable s at frequency $k={\sum }_i{r}_i{\omega }_i=\stackrel{\rightharpoonup }{r}\cdot {\stackrel{\rightharpoonup }{\omega }}^T$ [were $\stackrel{\rightharpoonup }{r}=(r_1,\dots ,r_n)$ and $\stackrel{\rightharpoonup }{\omega }=({\omega }_1,\dots ,{\omega }_n)$] can be estimated by Fourier coefficients in the θ-space as follows (see Appendix D in supplementary materials for details),

$$C_{(\stackrel{\rightharpoonup }{r}\cdot {\stackrel{\rightharpoonup }{\omega }}^T)}^{(s)}=C_{\stackrel{\rightharpoonup }{r}}^{(\theta )}+\sum _{{\stackrel{\rightharpoonup }{r}}^{\prime }}{C}_{{\stackrel{\rightharpoonup }{r}}^{\prime }}^{(\theta )}$$ (27)

where ${\stackrel{\rightharpoonup }{r}}^{\prime }$ is a vector different from $\stackrel{\rightharpoonup }{r}$ (i.e., $\stackrel{\rightharpoonup }{r}\ne {\stackrel{\rightharpoonup }{r}}^{\prime }$) with $\stackrel{\rightharpoonup }{r}\cdot {\stackrel{\rightharpoonup }{\omega }}^T={\stackrel{\rightharpoonup }{r}}^{\prime }\cdot {\stackrel{\rightharpoonup }{\omega }}^T$. If the frequency set {ω₁,…, ω_n} are strictly free of interferences to an order M as defined in Eq. (21), then ${\sum }_{{\stackrel{\rightharpoonup }{r}}^{\prime }}{C}_{{\stackrel{\rightharpoonup }{r}}^{\prime }}^{(\theta )}$ is negligible (see Appendix D in supplementary materials for details). Thus,

$$C_{(\stackrel{\rightharpoonup }{r}\cdot {\stackrel{\rightharpoonup }{\omega }}^T)}^{(s)}\approx C_{\stackrel{\rightharpoonup }{r}}^{(\theta )},\text{for}1\le |r_i|\le M.$$ (28)

Based on the partial variance estimation equation for multiple Fourier transformation in the θ-space [see Eq. (16)], the Fourier amplitude $|C_{00\dots r_i\dots 00}^{(\theta )}{|}^2$ is resulted from the main effect of parameter x_i. Therefore, based on Eq. (28), the Fourier amplitude $|C_{({\omega }_i{r}_i)}^{(s)}{|}^2$ over auxiliary variable s is also resulted from the main effect of parameter x_i. Based on Eqs. (16) and (28), the partial variances contributed by the main effects of parameters can be estimated as follows,

$${\widehat{V}}_{x_i}=\sum _{|r_i|=1}^M|C_{({\omega }_i{r}_i)}^{(s)}{|}^2.$$ (29)

Eq. (29) suggests that the partial variance contributed by the main effect of a specific parameter can be estimated by the sum of Fourier amplitudes at the characteristic frequency ω_i and its pth (p = 2, 3,…, M) harmonics over the auxiliary variable s. Based on Eqs. (16) and (28), we can also estimate the partial variances contributed by the second-order interaction effects, the third-order interaction effects and so on, until the nth order interaction effects as follows,

$$\begin{array}{l}{\widehat{V}}_{x_i{x}_j}={\displaystyle \sum _{|r_i|,|r_j|=1}^M|C_{({\omega }_i{r}_i+{\omega }_j{r}_j)}^{(s)}{|}^2}\\ {\widehat{V}}_{x_i{x}_j{x}_k}={\displaystyle \sum _{|r_i|,|r_j|,|r_k|=1}^M|C_{({\omega }_i{r}_i+{\omega }_j{r}_j+{\omega }_k{r}_k)}^{(s)}{|}^2}\\ \dots \\ {\widehat{V}}_{x_1,\dots ,x_n}={\displaystyle \sum _{|r_1|,\dots ,|r_n|=1}^M|C_{({\omega }_1{r}_1+\dots +{\omega }_n{r}_n)}^{(s)}{|}^2}.\end{array}$$ (30)

Eq. (30) suggests that partial variances contributed by higher-order interactions are resulted from linear combinations of characteristic frequencies. This has been implicitly shown or realized in the exploration of Fourier amplitudes at different frequencies for simple test models (Saltelli et al., 1999). However, our proof can corroborate the heuristic results and provide a better understanding of the FAST analysis. Based on Eq. (11), we can calculate sensitivity indices by the ratio of estimated partial variances to the sample variance of model output.

One key assumption for the estimation of partial variances in Eqs. (29) and (30) is that the selected characteristic frequency set {ω₁,…, ω_n} are strictly free of interferences to an order of M. The question is how to select the frequency set. This could be extremely difficult if the model has many parameters (e.g., 20 parameters). Cukier et al. (1975) provided a procedure on how to design a frequency set free of interferences to an order of four with Eq. (20). The designed frequency set free of interferences with Eq. (20) defines the interferences based on linear combinations of characteristic frequencies for at most (M + 1) parameters, while the frequency set strictly free of interferences as defined with Eq. (21) does not have that constraint. If we assume that higher-order interactions are negligible, then the frequency set selected with Eq. (20) can still provide a good approximation of the partial variances contributed by the first-order effects using Eq. (29), and can give us a reasonable estimation of the partial variances contributed by lower-order (<M) interaction effects of parameters using Eq. (30).

2.3. Simple random sampling

Fourier amplitudes will generally decrease quickly with an increasing harmonic. However, for highly nonlinear models, Fourier amplitudes can still be high for harmonics larger than four (i.e., r_i > 4) (Xu and Gertner, 2008). In order to estimate Fourier amplitudes at high harmonics in Eq. (30), we need to design a frequency set free of interferences to an order more than four. This would be very difficult for models with many parameters and may require an extremely large sample size (Cukier et al., 1975; Saltelli et al., 1999). Thus, we propose to estimate the partial variances in Eq. (16) by using simple random samples from the θ-space. The Fourier coefficients $C_{00\dots r_i\dots 00}^{(\theta )}$ in Eq. (16) are estimated by the sample mean using Eq. (15). Since we use a relatively small sample to explore the n-dimensional θ-space, the major concern is how much error there may be in the estimation of Fourier amplitudes (i.e., $|C_{r_1\dots r_n}^{(\theta )}{|}^2$ in Eq. (16)) by using random samples.

For the Fourier coefficient $C_{r_1\dots r_n}^{(\theta )}=a_{r_1,\dots ,r_n}^{(\theta )}-\mathbf{i}{b}_{r_1,\dots ,r_n}^{(\theta )}$, we show that the cosine Fourier coefficient $a_{r_1\dots r_n}^{(\theta )}$ and sine Fourier coefficient $b_{r_1\dots r_n}^{(\theta )}$ approximately follow normal distributions (see Eq. (E12) in Appendix E in supplementary materials for details)

$$\begin{array}{c}{\widehat{a}}_{r_1\dots r_n}^{(\theta )}\sim \stackrel{\dots }{N}(a_{r_1\dots r_n}^{(\theta )},V({\widehat{a}}_{r_1\dots r_n}^{(\theta )})),\\ {\widehat{b}}_{r_1\dots r_n}^{(\theta )}\sim \stackrel{\dots }{N}(b_{r_1\dots r_n}^{(\theta )},V({\widehat{b}}_{r_1\dots r_n}^{(\theta )}))\end{array}$$ (31)

where $\stackrel{\dots }{N}(u,\upsilon )$ represents a normal distribution with mean u and variance υ and

$$\begin{array}{c}V({\widehat{a}}_{r_1\dots r_n}^{(\theta )})=\frac{1}{N}V[g(G({\theta }_1),\dots ,G({\theta }_n))cos(r_1{\theta }_1+\dots +r_n{\theta }_n)],\\ V({\widehat{b}}_{r_1\dots r_n}^{(\theta )})=\frac{1}{N}V[g(G({\theta }_1),\dots ,G({\theta }_n))sin(r_1{\theta }_1+\dots +r_n{\theta }_n)].\end{array}$$ (32)

Thus, the estimation errors of cosine and sine Fourier coefficients decay at a rate of $\frac{1}{\sqrt{N}}$ with an increasing sample size N. The estimated Fourier amplitude $|{\widehat{C}}_{r_1\dots r_n}^{(\theta )}{|}^2$ based on Eq. (15) is a biased estimator for $|C_{r_1\dots r_n}^{(\theta )}{|}^2$ (see Eq. (E11) in Appendix E in supplementary materials). Namely,

$$E\left(|{\widehat{C}}_{r_1\dots r_n}^{(\theta )}{|}^2\right)=|C_{r_1\dots r_n}^{(\theta )}{|}^2+{\mathit{\delta }}_e$$ (33)

where

$${\mathit{\delta }}_e=\frac{1}{N}\left\{E{\left[g(G({\theta }_1),\dots ,G({\theta }_n))\right]}^2-|C_{r_1,\dots ,r_n}^{(\theta )}{|}^2\right\}.$$ (34)

The bias δ_e is mainly dominated by the second moment of model output y, in view that $|C_{r_1\dots r_n}^{(\theta )}{|}^2$ is generally much smaller because $|C_{r_1\dots r_n}^{(\theta )}{|}^2$ is just a proportion of the variance of model output. In order to reduce the bias induced by sampling errors, we need to increase the sample size N. Generally, we estimate the partial variances based on the sum of Fourier amplitudes at a fundamental frequency and its higher harmonics. At higher harmonics, there will be fewer signals for the contributed partial variances, and thus higher proportion of noise signal δ_e. In order to reduce the effect of sampling errors on partial variance estimation, we also need to limit the Fourier amplitude calculation to a certain maximum harmonic order (M, generally four or six in practice). Xu and Gertner (2008) proposed a method to check the Fourier amplitudes and select maximum harmonics where Fourier amplitudes begin to stabilize. For parameters with lower variance contribution, Xu and Gertner (2008) recommended using a relatively small maximum harmonic order (e.g., 1 or 2), since they are more subject to random errors.

For a better exploration of the parameter space, it is also desirable to use different forms of the search function in Eq. (5) for different parameters as long as the search function can generate samples in the parameter space based on samples in the θ-space. For example, we can have

$$x_i=G_i({\theta }_i)=F^{-1}\left(\frac{1}{2}+arcsin(sin({\omega }_i{\theta }_i))\right)$$ (35)

where ω_i is a search frequency. The search frequency set {ω_i} is not necessarily designed to be free of interferences since we did not use this to distinguish partial variances contributed by different parameters. Since the model output y becomes a periodic function of {θ_i} with strong signals at the frequencies {ω_i}, partial variances contributed by different parameters can be estimated by Fourier amplitudes at the frequencies {ω_i} and their harmonics. Namely,

$$\begin{array}{l}{\widehat{V}}_{x_i}={\displaystyle \sum _{|r_i|=1}^M|{\widehat{C}}_{00\dots ({\omega }_i{r}_i)\dots 00}^{(\theta )}{|}^2}\\ {\widehat{V}}_{x_i{x}_j}={\displaystyle \sum _{|r_i|,|r_j|=1}^M|{\widehat{C}}_{00\dots ({\omega }_i{r}_i)\dots ({\omega }_j{r}_j)\dots 00}^{(\theta )}{|}^2}\\ \dots \\ {\widehat{V}}_{x_1,\dots ,x_n}={\displaystyle \sum _{|r_1|,\dots ,|r_n|=1}^M|{\widehat{C}}_{({\omega }_1{r}_1)\dots ({\omega }_n{r}_n)}^{(\theta )}{|}^2},\end{array}$$ (36)

where M is a maximum harmonic order specified by the user (see text below for specification of M). Based on Eq. (11), we can calculate the sensitivity indices using the ratios of estimated partial variances to the sample variance of model output y.

A statistically robust approach for maximum harmonic order (i.e., M) selection is to first set a relatively large M (e.g., 10 or 20). Then, a statistical test can be constructed to select cosine and sine Fourier coefficients significantly larger or smaller than zero for the calculation of Fourier Amplitudes (i.e., $|{\widehat{C}}_{r_1\dots r_n}^{(\theta )}{|}^2={({\widehat{a}}_{r_1,\dots ,r_n}^{(\theta )})}^2+{({\widehat{b}}_{r_1,\dots ,r_n}^{(\theta )})}^2$). Under the null hypothesis that the true cosine Fourier coefficient $a_{r_1\dots r_n}^{(\theta )}$ and sine Fourier coefficient $b_{r_1\dots r_n}^{(\theta )}$ are zeros, a z-score test statistic for ${\widehat{a}}_{r_1\dots r_n}^{(\theta )}$ and ${\widehat{b}}_{r_1,\dots ,r_n}^{(\theta )}$ can be defined as,

$$\begin{array}{c}{Z}_a=\frac{{\widehat{a}}_{r_1,\dots ,r_n}^{(\theta )}}{\sqrt{\widehat{V}({\widehat{a}}_{r_1,\dots ,r_n}^{(\theta )})}},\\ Z_b=\frac{{\widehat{b}}_{r_1,\dots ,r_n}^{(\theta )}}{\sqrt{\widehat{V}({\widehat{b}}_{r_1,\dots ,r_n}^{(\theta )})}},\end{array}$$ (37)

which follow standard normal distributions in view that ${\widehat{a}}_{r_1,\dots ,r_n}^{(\theta )}$ and ${\widehat{b}}_{r_1,\dots ,r_n}^{(\theta )}$ follow normal distributions (assuming a relatively large sample size N) with variances $\widehat{V}({\widehat{a}}_{r_1\dots r_n}^{(\theta )})$ and $\widehat{V}({\widehat{b}}_{r_1\dots r_n}^{(\theta )})$, respectively (see Eq. (31) for details). The sample variance of a random variable is represented by $\widehat{V}[.]$. Specifically, the sample variance of ${\widehat{a}}_{r_1\dots r_n}^{(\theta )}$ and ${\widehat{b}}_{r_1\dots r_n}^{(\theta )}$ [i.e., $\widehat{V}({\widehat{a}}_{r_1\dots r_n}^{(\theta )})$ and $\widehat{V}({\widehat{a}}_{r_1\dots r_n}^{(\theta )})$] can be estimated based on Eq. (32) as follows,

$$\begin{array}{c}V({\widehat{a}}_{r_1,\dots ,r_n}^{(\theta )})=\frac{1}{N^2}{\displaystyle \sum _{j=1}^N}[g^2(G({\theta }_1^{(j)}),\dots ,G({\theta }_n^{(j)})){cos}^2(r_1{\theta }_1^{(j)}+\dots +r_n{\theta }_n^{(j)})]-\frac{1}{N}{({\widehat{a}}_{r_1,\dots ,r_n}^{(\theta )})}^2\\ V({\widehat{b}}_{r_1,\dots ,r_n}^{(\theta )})=\frac{1}{N^2}{\displaystyle \sum _{j=1}^N}[g^2(G({\theta }_1^{(j)}),\dots ,G({\theta }_n^{(j)})){sin}^2(r_1{\theta }_1^{(j)}+\dots +r_n{\theta }_n^{(j)})]-\frac{1}{N}{({\widehat{b}}_{r_1,\dots ,r_n}^{(\theta )})}^2.\end{array}$$ (38)

If |Z_a| is larger than Z_c(α), where Z_c(α) is the critical value based on a standard normal distribution at a significance level α, we reject the null hypothesis that true cosine Fourier coefficient $a_{r_1\dots r_n}^{(\theta )}$ is zero. The corresponding alternative hypothesis states that $a_{r_1\dots r_n}^{(\theta )}$ is larger than zero if $a_{r_1\dots r_n}^{(\theta )}>Z_{c(\alpha )}$ or $a_{r_1\dots r_n}^{(\theta )}$ is smaller than zero if $a_{r_1\dots r_n}^{(\theta )}<-Z_{c(\alpha )}$. Similarly, if |Z_b | is larger than Z_c(α), we reject the null hypothesis that true sine Fourier coefficient $b_{r_1\dots r_n}^{(\theta )}$ is zero. To reduce the effect of sampling error on Fourier amplitudes estimation in Eq. (16), we calculate the Fourier amplitudes only using the Fourier coefficients significantly larger or smaller than zero (i.e., |Z_a| > Z_c(α) or |Z_b| > Z_c(α)).

We have constructed hypothesis tests with Eq. (37) to select cosine and sine Fourier coefficients significantly larger or smaller than zero for the calculation of Fourier amplitudes. This relaxes the requirement to select an accurate maximum harmonic order M in our calculation of partial variances in Eq. (36). Namely, we can select a relatively large M and use statistical tests to avoid overestimation of sensitivity indices by excluding those cosine and sine Fourier coefficients not significantly larger or smaller than zero. However, for the calculation of partial variances contributed by higher-order interactions, we recommend that the user select a relatively small M (e.g. 3 or 4). For higher-order interactions, there are too many harmonics with a large maximum harmonic order M. For example, for the third-order interactions, if we select M = 5, then there are 1000 cosine/sine Fourier coefficients to be estimated based on Eq. (36) [Note that the cosine and sine Fourier coefficients at frequency (r₁,…, r_n) are the same as those at frequency (−r₁,…, −r_n) except for sign differences]. This will make it challenging to conduct the hypothesis tests. Let us assume that there were no third-order interactions in the model. Even if we specify a small (e.g., 1%) type I error (the error of rejecting the null hypothesis when the null hypothesis is true), there is still the possibility that 10 out of 1000 cosine and sine Fourier coefficients will be randomly selected. This could overestimate the partial variances contributed by higher-order interactions. We recommend that the user limit the number of estimated cosine and sine Fourier coefficients to be less than 100, so that there is less than one harmonic to be randomly selected at a significance level of 0.01 given that main effects or interaction effects of parameters have no contributions to uncertainty in the model output. This suggests that we need to limit M ≤ 50 for the first-order effects; M ≤ 5 for the second-order interaction effects; M ≤ 2 for the third-order interaction effects; and M ≤ 1 for the fourth-order interaction effects.

2.4. Random balance design sampling

Tarantola et al. (2006) introduced a random balance design sampling method so that FAST does not need a frequency set free of interferences to a user-specified order of M. Although the original algorithm is proposed by permutation over auxiliary variable s, it is equivalent that we first draw N grid samples for each {θ_i},

$$\left\{{\theta }_1^{(1)},\dots ,{\theta }_n^{(N)}|{\theta }_i^{(j)}={\theta }_0+\frac{2\pi }{N}(j-1),j=1,\dots ,N\right\}$$ (39)

where θ₀ is randomly drawn from $[0,\frac{\pi }{N}]$ so that the grid sample for θ_i can ergodically explore between 0 and 2π as N → ∞. Then the samples are randomly permuted to form N samples in the θ-space. In this way, similar to simple random sampling, the random balance design sampling draws random samples in the high-dimensional θ-space. Thus, estimation errors for Fourier coefficients in the θ-space using random balance design sampling will be similar to those based on simple random sampling. However, by using grid samples for each individual parameter, estimation errors for partial variances contributed by the main effects can be much smaller than those estimated using simple random sampling (see Appendix F in supplementary materials). For a Fourier coefficient $C_{00\dots r_i\dots 00}^{(\theta )}=a_{00\dots r_i\dots 00}^{(\theta )}-\mathbf{i}{b}_{00\dots r_i\dots 00}^{(\theta )}$, the estimation errors of the cosine Fourier $a_{00\dots r_i\dots 00}^{(\theta )}$ coefficient and sine Fourier coefficient, $b_{00\dots r_i\dots 00}^{(\theta )}$ approximately follow normal distributions based on the Central Limit Theorem (see Eq. (F12) in Appendix F in supplementary materials). Namely,

$$\begin{array}{c}{\widehat{a}}_{00\dots r_i\dots 00}^{(\theta )}\sim \stackrel{\dots }{N}\left(a_{00\dots r_i\dots 00}^{(\theta )},\frac{V(\xi -x_i)}{2N}\right),\\ {\widehat{b}}_{00\dots r_i\dots 00}^{(\theta )}\sim \stackrel{\dots }{N}\left(b_{00\dots r_i\dots 00}^{(\theta )},\frac{V(\xi -x_i)}{2N}\right),\end{array}$$ (40)

where

$$V({\xi }_{-x_i})=V^{(x_1,\dots ,x_n)}-V^{(x_i)}.$$ (41)

Based on Eqs. (F7) and (F10), it is shown that the estimation errors for Fourier coefficient $c_{00\dots r_i\dots 00}^{(\theta )}$ using random balance design sampling [see Eq. (40)] is much smaller than that using simple random sampling [see Eq. (31)] (see Appendix F in supplementary materials for details).

In order to reduce the effect of sampling errors on partial variance estimation in Eq. (36), test statistics with Eq. (37) can be constructed to select cosine and sine Fourier coefficients significantly larger or smaller than zero. However, for partial variances contributed by the first-order effects, the variance of estimated Fourier coefficients can be improved based on Eq. (40). For the estimation of V (ξ_−xi) in Eq. (40), we need to have a preliminary estimation of V^(x_i). In this paper, we propose a conservative preliminary estimation of V^(x_i) as follows,

$${\stackrel{\sim }{V}}^{(x_i)}=\sum _{|r_i|=1}^{\stackrel{\sim }{M}}|{\widehat{C}}_{00\dots ({\omega }_i{r}_i)\dots 00}^{(\theta )}{|}^2$$ (42)

where M̃ is a relatively small harmonic order (e.g., 4), under which the amplitudes have a relatively small proportion of errors. In order to improve the estimation accuracy of V^(x_i), the statistical test in Eq. (37) for simple random sampling can be used to select those cosine and sine Fourier coefficients significantly larger or smaller than zero for the calculation of Fourier amplitudes. Based on the preliminary estimation of V^(x_i), we can calculate the sample variances of Fourier coefficients in Eq. (37). Namely,

$$\widehat{V}({\widehat{a}}_{r_1\dots r_n}^{(\theta )})=\widehat{V}({\widehat{b}}_{r_1,\dots ,r_n}^{(\theta )})=\frac{1}{2N}[{\widehat{V}}^{(x_1\dots x_n)}-{\stackrel{\sim }{V}}^{(x_i)}],$$ (43)

where Vˆ^{(x_i,…,x_n)} is the sample variance of model output.

It can also be shown that the estimated Fourier amplitude $|{\widehat{C}}_{r_1\dots r_n}^{(\theta )}{|}^2$ based on Eq. (15) is a biased estimator for $|{\widehat{C}}_{r_1\dots r_n}^{(\theta )}{|}^2$(see Eq. (F11) in Appendix F in supplementary materials for details). Namely,

$$E(|{\widehat{C}}_{00\dots r_i\dots 00}^{(\theta )}{|}^2)=|C_{00\dots r_i\dots 00}^{(\theta )}{|}^2+\frac{V({\xi }_{-x_i})}{N}.$$ (44)

Notice that V (ξ_−xi) is relatively small for parameters with large variance contributions (i.e., larger values of V^(x_i) in Eq. (41)) and is relatively large for parameters with low variance contributions. This suggests that the estimation bias is relatively low for parameters with large variance contributions and relatively high for parameters with small variance contributions.

3. Comparison of different sampling schemes

In Section 2, we have introduced different sampling approaches including: (1) search-curve based sampling using an auxiliary variable s (see Section 2.2); (2) simple random sampling (see Section 2.3); and (3) random balance design sampling (see Section 2.4). For the simple random sampling and random balance design sampling approaches, estimation errors for the partial variances in Eq. (16) are mainly resulted from the Fourier coefficient estimation errors in Eq. (15). Since estimation errors for Fourier coefficients $C_{00\dots r_i\dots 00}^{(\theta )}$ using random balance design sampling is much smaller than that using simple random sampling with a relatively large sample size (see Appendix F in supplementary materials for details), the estimation precision for first-order sensitivity indices using random balance sampling should be much higher. For the simple random sampling, the estimation bias for the Fourier amplitude $|C_{r_1,\dots ,r_n}^{(\theta )}{|}^2$ is related to the second moment of model output y (i.e., $\frac{E{\left[g(G({\theta }_1),\dots ,G({\theta }_n))\right]}^2}{N}$, see Eq. (33) for details). For the random balanced design sampling, the estimation bias for the Fourier amplitude $|C_{00\dots r_i\dots 00}^{(\theta )}{|}^2$ is $\frac{V({\xi }_{-x_i})}{N}$ (see Eq. (44) for details). Since V(ξ_−xi) is only a fraction of E [g(G(θ₁),…, G(θ_n))]², estimation errors of partial variances contributed by the main effects using random balance design sampling should be smaller than those using simple random sampling. For the search-curve based sampling approach, there are two sources of estimation errors for the partial variance calculation in Eq. (16): (1) the interference errors in Eq. (27); and (2) the numerical integral errors for Fourier coefficients in Eq. (26). By using the rectangle rule for an one-dimensional integral, the Fourier coefficient estimation errors decay at a rate of $\frac{1}{N^2}$ with an increasing sample size N. For a relatively large sample size, the Fourier coefficient estimation errors are relatively small. Thus, the main sources of estimation errors are due to the interferences among frequencies. If the frequency set is designed to be strictly free of interferences to a high order M, then the traditional search-curve sampling should give better estimation of sensitivity indices compared to simple random sampling and random balance design sampling.

For the purpose of illustration, we compared the performance of the three sampling approaches using a simple test model,

$$y=\sum _{i=1}^3(i{x}_i^2)+x_1{x}_2+2x_2{x}_3+3x_1{x}_3+x_1{x}_2{x}_3$$ (45)

where x₁, x₂, and x₃ are three independent parameters of the model. We assume all parameters follow standard normal distributions. Although the model is simple, it is representative since it is nonlinear and non-monotonic. For this simple model, we can analytically calculate the partial variances in the parameter space as defined in Eq. (6) (see Appendix G in supplementary materials and Table 1 for details). For each sampling approach, we compare the mean values of sensitivity indices (used as a measure of bias when compared to the analytical value) and their standard deviations (used as a measure of estimation precision) using 20 replicates of samples with different sample sizes (1000, 2000, 5000 and 10,000). For each replicate generated through the traditional search-curve sampling, we have a different frequency set free of interferences to an order of four (see Table S1 in supplementary materials).

Table 1.

Analytical partial variances and sensitivity indices for the test model.

Effects	Partial variance	Sensitivity
Vx1	2	0.047
Vx2	8	0.186
Vx3	18	0.419
Vx1x2	1	0.023
Vx1x3	9	0.209
Vx2x3	4	0.093
Vx1x2x3	1	0.023

Below we provide a summary of the FAST procedures using the different sampling approaches to better illustrate the FAST analysis.

• FAST procedure for search-curve based sampling

  1. Define a set of frequencies free of interferences to an order to M (M = 4 in this test case);

  2. Generate grid samples for an auxiliary variable s using Eq. (19) and the corresponding sample for parameters using the search curve in Eq. (18) and search function in Eq. (5);

  3. Run the model based on the sampled values of parameters;

  4. Calculate the partial variances based on Eq. (30) and the corresponding sensitivity indices based on Eq. (11). The first-order sensitivity indices are calculated based on M = 4. In order to reduce the effect of inference error, the second-order and the third-order sensitivity indices are calculated based on M = 1.

• FAST procedure using simple random sampling

  1. Draw independent random samples in the θ-space $(K_{\theta }^n=\{{\theta }_{1,\dots ,}{\theta }_n|0<{\theta }_i<2\pi ,i=1,\dots ,n\});$

  2. Generate corresponding random samples in the parameter space using search functions in Eq. (5) and the sample in the θ-space;

  3. Run the model based on the samples in the parameter space;

  4. Calculate the partial variances based on Eq. (36) and the corresponding sensitivity indices with Eq. (11). Statistical tests in Eq. (37) are used to select Fourier coefficients significantly larger or smaller than zero for the estimation of Fourier amplitudes in Eq. (36). In this test case, we select the maximum harmonic order M = 20 for partial variances contributed by the first-order interaction effects, M = 5 for the second-order interaction effects, and M = 2 for the third-order interaction effects. The statistical tests are based on a significance level of 0.01.

• FAST procedure using random balance design sampling

  1. Draw N grid samples for {θ_i} using Eq. (39), which is then randomly permuted to form a random sample in the θ-space;

  2. Generate a corresponding random sample in the parameter space using search functions in Eq. (5) and the sample in the θ-space;

  3. Run the model based on samples in the parameter space;

  4. Calculate the partial variances based on Eq. (36) and the corresponding sensitivity indices with Eq. (11). Statistical tests in Eq. (37) are used to select Fourier coefficients significantly larger or smaller than zero for the estimation of Fourier amplitudes in Eq. (36). For partial variances contributed by the first-order effects, we calculate sample variances of Fourier coefficients by Eq. (43) with M̃ = 4. For the partial variances contributed by higher-order interactions, we calculate sample variances of Fourier coefficients using Eq. (38). We select the maximum harmonic order M = 20 for partial variances contributed by the first-order interaction effects, M = 5 for the second-order interaction effects, and M = 2 for the third-order interaction effects. The statistical tests are based on a significance level of 0.01.

4. Results

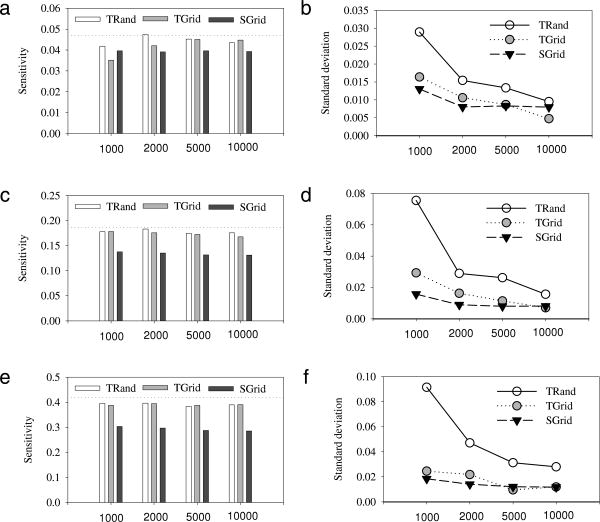
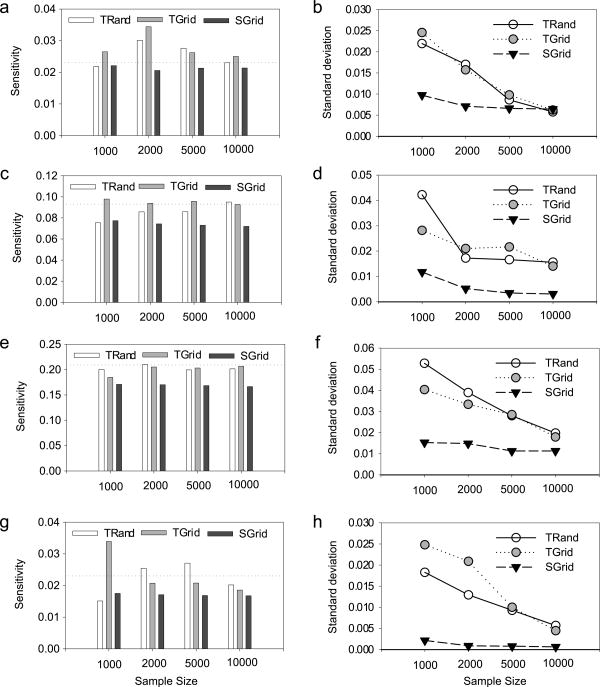
Our results based on the simple test model with Eq. (45) show that, estimated sensitivity indices using the FAST method are close to the analytical results. However, they are commonly underestimated for all three sampling approaches (Figs. 1(a), (c), (e) and 2 (a), (c), (e), (g)). The underestimation of sensitivity indices by simple random sampling and random balanced design sampling are due to the fact that we employ statistical hypothesis tests to exclude relatively low Fourier amplitudes. It is noteworthy that, even though the Fourier amplitudes are biased as shown in Eqs. (33) and (44), the bias of estimated sensitivity indices is small by using statistical hypothesis tests. We did not detect significant difference in bias between simple random sampling and random balanced design sampling, because of two reasons. First, the statistical hypothesis tests reduce the bias that occurred in partial variance estimation by excluding small Fourier Amplitudes. Second, there is not much difference between the variance (43) and second moment of model output y (∼78), which are relatively small compared to the sample size. The underestimation for the search-curve based sampling is higher than that for simple random sampling and random balance design sampling, since the search-curve based sampling limits maximum harmonic order to four, which is implicitly determined by the specified frequency sets.

Fig. 1.

Comparison of different sampling approaches (SGrid = search-curve based sampling using the auxiliary variables s, TRand = simple random sampling in θ-space; TGrid = random balance design sampling in the θ-space) for the first-order sensitivity indices with different sample sizes (1000, 2000, 5000 and 10,000). The panels (a), (c) and (e) represent the sample mean (based on 20 replicates) of the first-order sensitivity indices for parameters x₁, x₂ and x₃, respectively. The dotted horizontal reference lines represent the analytical sensitivity indices in Table 1. The panels (b), (d) and (f) represent the corresponding standard deviations for the estimated sensitivity indices.

Fig. 2.

Comparison of different sampling approaches (SGrid=search-curve based sampling using the auxiliary variable s, TRand=simple random sampling in θ-space, TGrid=random balance design sampling in the θ-space) for higher-order sensitivity indices with different sample sizes (1000, 2000, 5000 and 10,000). The panels (a), (c), (e) and (g) represent the sample mean (based on 10 replicates) of higher-order sensitivity indices for the interactions between x₃ and x₂, x₁ and x₃, x₁ and x₃, x₁, x₂ and x₃, respectively. The dotted horizontal reference lines represent the analytical sensitivity indices in Table 1. The panels (b), (d), (f) and (h) represent the corresponding standard deviations for the calculated sensitivity indices.

The standard deviations of estimated sensitivity indices generally decrease with sample size (Fig. 1(b), (d), (f) and Fig. 2(b), (d), (f), (h)), which suggests that estimation precision increases as the sample size increases. The standard deviations are measures of estimation precision for sensitivity indices. For the search-curve based sampling, standard deviations of estimated sensitivity indices do not decrease much when the sample size is larger than 2000. This suggests that the increase in sample size does not greatly improve estimation precision (or reduce estimation error) when the sample size is relatively large, in view that the numerical integral error decreases at a rate of squared sample size. If the sample size is less than 10,000, the standard deviations based on random balance design sampling are generally lower than those based on simple random sampling for the first-order sensitivity indices (Fig. 1(b), (d), (f)). This suggests that random balance design sampling can substantially increase the precision of the first-order sensitivity indices when the sample size is relatively small. However, for the second-order and third-order sensitivity indices, standard deviations based on random balance design sampling are close to those based on simple random sampling. This suggests that random balance design sampling does not improve estimation precision for higher-order sensitivity indices.

If we combine the bias and precision into a statistic of root mean square error (RMSE: $\sqrt{E{({\widehat{\alpha }}_{x_i}-{\alpha }_{x_i})}^2}$), we can see that the RMSE for search-curve based sampling can be much larger than that based on simple random sampling and random balance design sampling (Fig. S1(b), (c), (f) in Supplementary Materials), due to its large underestimation for parameters with relatively large sensitivity indices (Figs. 1(c), (e) and 2(e)).

5. Discussion

Our paper shows that FAST can theoretically be used to estimate higher-order sensitivity indices, although it would be difficult for estimating higher-order sensitivity indices (fourth-order and higher) due to the larger number of Fourier coefficients to be estimated. It is a common assumption in experimental design that the higher-order interactions are trivial by specifying two levels for each parameter/factor assuming linear effects of factors on model outputs (Mason et al., 2003, Chapter 7). However, that may not be the case for the FAST analysis, where parameters have many levels and nonlinear relationships between model parameters and outputs may exist. If the user does care about fourth-order and higher interactions, please refer to Saltelli et al. (1999) for calculating a total sensitivity index for a parameter incorporating all interactions with other parameters.

Our derivation shows that, for partial variances contributed by the main or interaction effects of parameters in simple random sampling and partial variances contributed by higher-order interactions in random balance design sampling, the estimation biases for Fourier amplitudes are related to the second moment of model output, specifically, $\frac{E{\left[g(G({\theta }_1),\dots ,G({\theta }_n))\right]}^2}{N}$ (see Eq. (33) for details). Since the sensitivity index is calculated based on the ratio of sum of Fourier amplitudes to variance of model output σ² (see Eq. (11) for details), it is possible that the calculated sensitivity index is larger than one if $\frac{E{\left[g(G({\theta }_1),\dots ,G({\theta }_n))\right]}^2}{N}$ is much larger than σ². In order to overcome this potential problem, we recommend that the model output be centered by the sample mean and/or scaled by the standard deviation of the model output, so that $\frac{E{\left[g(G({\theta }_1),\dots ,G({\theta }_n))\right]}^2}{N}$ is generally smaller than the variance σ². By using the centered model outputs, we can also have lower estimation errors for Fourier coefficients (i.e., smaller standard errors with Eq. (38)) and thus higher accuracy and precision for the estimated partial variances. Our recommendation to subtract the mean of the model output is a standard procedure to reduce the error in numerical estimates (e.g. Sobol, 2001).

In our derivation, we assume that models are deterministic. Namely, the output of the model is only determined by model parameters. However, in real applications, it is common to have stochastic components in the model to represent natural variability. For readers with interests in applying FAST to stochastic models, please refer to Appendix H in supplementary materials for further discussion. In our derivation, we assume that model parameters are independent. However, the model parameters are commonly correlated. For readers with interests in applying FAST for models with correlated parameters, please refer to Appendix I in supplementary materials for further discussion.

6. Conclusion

The FAST analysis is mainly confined to the estimation of partial variances contributed by the main effects of model parameters. In this paper, we show that the FAST analysis can be used to estimate partial variances contributed by both main effects and interaction effects of parameters for different sampling approaches (i.e., the search-curve based sampling, simple random sampling, and random balance design sampling). We also analytically calculate the potential errors and biases in the estimation of partial variances. We found that compared to simple random sampling and random balance design sampling, sensitivity indices estimated by search-curve based sampling generally have higher precision (i.e., smaller standard deviations), but larger underestimations, given that frequency sets are selected to be free of interferences to an order of four. Compared to simple random sampling, random balance design sampling generally provides higher estimation precision for partial variances contributed by the main effects of parameters. In view of the potentially large estimation errors for calculated sensitivity indices resulting from a large mean and a low variance of the model output, we recommend that the model output be centered by its sample mean to improve their estimation accuracy. The theoretical derivation of variance decomposition and calculation of estimation errors and biases of partial variances in this paper can help us better understand the FAST method and provide a fundamental basis for FAST applications (e.g., calculation of higher-order sensitivity indices) and further improvements in the future.