Protein ranking: From local to global structure in the protein similarity network

Abstract

Biologists regularly search databases of DNA or protein sequences for evolutionary or functional relationships to a given query sequence. We describe a ranking algorithm that exploits the entire network structure of similarity relationships among proteins in a sequence database by performing a diffusion operation on a precomputed, weighted network. The resulting ranking algorithm, evaluated by using a human-curated database of protein structures, is efficient and provides significantly better rankings than a local network search algorithm such as psi-blast.

Pairwise sequence comparison is the most widely used application of bioinformatics. Subtle sequence similarities frequently imply structural, functional, and evolutionary relationships among protein and DNA sequences. Consequently, essentially every molecular biologist working today has searched an online database of biosequences. This search process is analogous to searching the World Wide Web with a search engine such as Google: the user enters a query (a biological sequence or a word or phrase) into a web form. The search engine then compares the query with each entry in a database, and returns to the user a ranked list, with the most relevant or most similar database entry at the top of the list.

The World Wide Web consists of a network of documents connected to one another by means of hypertext links. A database of protein sequences can also be usefully represented as a network, in which edges may represent functional, structural, or sequence similarity. Two protein sequences are considered similar if they contain subsequences that share more similar amino acids than would be expected to occur by chance. We refer to the network of sequence similarities as a protein similarity network.

Early algorithms for detecting sequence similarities did not exploit the structure of the protein similarity network at all, but focused instead on accurately defining the individual edges of the network (1–3). Subsequent work used statistical models based on multiple alignments to model the local structure of the network (4, 5) and to perform local search through the protein similarity network by using short paths (6), average- or single-linkage scoring of inbound edges (7, 8), and iterative model-based search (9, 10). The popular psi-blast (11) algorithm falls into the latter category: psi-blast builds an alignment-based statistical model of a local region of the protein similarity network and then iteratively collects additional sequences from the database to be added to the alignment.

The critical innovation that led to the success of the Google search engine is its ability to exploit global structure by inferring it from the local hyperlink structure of the Web. Google's pagerank algorithm (12) models the behavior of a random web surfer, who clicks on successive links at random and also periodically jumps to a random page. The web pages are ranked according to the probability distribution of the resulting random walk. Empirical results show that pagerank is superior to the naive, local ranking method, in which pages are simply ranked according to the number of inbound hyperlinks.

We demonstrate that a similar advantage can be gained by including information about global network structure in a protein sequence database search algorithm. In contrast to iterative protein database search methods such as psi-blast, which compute the local structure of the protein similarity network on the fly, the rankprop algorithm begins from a precomputed protein similarity network, defined on the entire protein data-base. Querying the database consists of adding the query sequence to the protein similarity network and then propagating link information outward from the query sequence. After propagation, database proteins are ranked according to the amount of link information they received from the query. This algorithm ranks the data with respect to the intrinsic cluster structure (13, 14) of the network. We evaluate the rankprop output by using a 3D-structure-based gold standard, measuring the extent to which known homologs occur above nonhomologs in the ranked list. Our experiments suggest that rankprop's ranking is superior to the ranking induced by the direct links in the original network.

The protein similarity network represents the degree of similarity between proteins by assigning weights to each edge. The degree of similarity between two sequences is commonly summarized in an E value, which is the expected number of times that this degree of sequence similarity would occur in a random database of the given size. By using a weighting scheme that is a function of the E value, an edge connecting two similar sequences is given a large weight, and vice versa.

To accommodate edge weights, the rankprop algorithm adopts recently described diffusion techniques (15) from the field of machine learning, which are closely related to the spreading activation networks of experimental psychology (16, 17). rankprop takes as input a weighted network on the data, with one node of the network designated as the query. In the protein ranking problem, the edges of the network are defined by using psi-blast. The query is assigned a score, and this score is continually pumped to the remaining points by means of the weighted network. During the diffusion process, a protein P pumps to its neighbors at time t the linear combination of scores that P received from its neighbors at time t - 1, weighted by the strengths of the edges between them. The diffusion process continues until convergence, and the points are ranked according to the scores they receive. The rankprop algorithm is described formally in Fig. 1. This algorithm provably converges, and an exact closed form solution can be found (see Supporting Information, which is published on the PNAS web site).

Fig. 1.

The rankprop algorithm. Given a set of objects (in this case, proteins) X = x_1,..., x_m, let x₁ be the query and x_2,..., x_m be the database (targets) we would like to rank. Let K be the matrix of object–object similarities, i.e., K_ij gives a similarity score between x_i and x_j, with K normalized so that 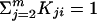for all i. For computational efficiency, we set K_1i = K_i1 for all i, so that we can compute weights involving the query using a single execution of psi-blast. Let y_i, i = 2,..., m, be the initial ranking “score” of a target. In practice, for efficiency, the algorithm is terminated after a fixed number I of iterations, and y_i(I) is used as an approximation of 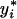. The parameter α ∈ [0,1] is set a priori by the user. For α = 0, no global structure is found, and the algorithm's output is just the ranking according to the original distance metric. These experiments use α = 0.95, looking for clear cluster structure in the data.

Methods

We tested the quality of the protein rankings produced by rankprop, using the human-annotated SCOP database of protein 3D structural domains as a gold standard (18). SCOP has been used as a gold standard in many previous studies (19–21). Sequences were extracted from version 1.59 of the database, purged by using the web site http://astral.berkeley.edu so that no pair of sequences share more than 95% identity. For the purposes of selecting the rankprop parameter σ, the resulting collection of 7,329 SCOP domains was split into two portions: 379 superfamilies (4,071 proteins) for training and 332 (2,899 proteins) for testing. Note that training and testing sequences never come from the same superfamily. The SCOP database is organized hierarchically into classes, folds, superfamilies, and families. For the purposes of this experiment, two domains that come from the same superfamily are assumed to be homologous, and two domains from different folds are assumed to be unrelated. For pairs of proteins in the same fold but different superfamilies, their relationship is uncertain, and so these pairs are not used in evaluating the algorithm.

Three protein similarity networks were computed by using the blast and psi-blast (version 2.2.2) algorithms. Two networks were defined by applying blast and psi-blast to a database comprised only of the 7,329 SCOP domains. An additional network was created by applying psi-blast to a larger database that also included all 101,602 proteins from swiss-prot (version 40). In each case, the programs were run by using the default parameters, including the blosum 62 matrix, but with an E value threshold for reporting results of 10,000. psi-blast was allowed to run a maximum of six iterations, which previous work indicates is sufficient for good performance (21), using the default E value threshold for inclusion in the model of 0.005. Each of these networks induces a ranking with respect to each query sequence.

Finally, we applied rankprop to the larger psi-blast protein similarity network. In the network K used by rankprop, the weight K_ij associated with a directed edge from protein i to protein j is exp(-S_j(i)/σ), where S_j(i) is the E value assigned to protein i given query j. The value of σ = 100 is chosen by using the training set (see supporting information). For efficiency, the number of outgoing edges from each node is capped at 1000, unless the number of target sequences with E values <0.05 exceeds 1000. For each query, rankprop runs for 20 iterations, which brings the algorithm close to convergence (see supporting information).

We measure the performance of a protein database search algorithm by using a modified version of the receiver operating characteristic (ROC) score (22). The ROC score is the area under a curve that plots false-positive rate versus true-positive rate for various classification thresholds. The ROC score thus measures, for a single query, the quality of the entire ranking produced by the algorithm. In practice, only the top of this ranking is important. Therefore, we compute the ROC₅₀ score (23), which is the area under the ROC curve up to the first 50 false-positives. A value of 1 implies that the algorithm successfully assigns all of the true relationships higher scores than the false relationships. For a random ranking of these data, the expected ROC₅₀ score is close to 0 because most of the sequences are not related to the query.

Results

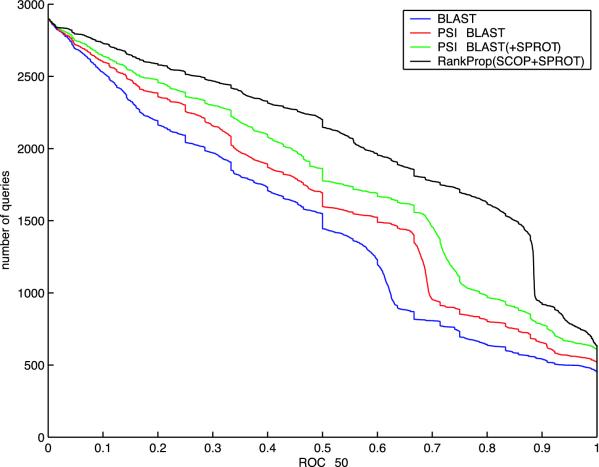
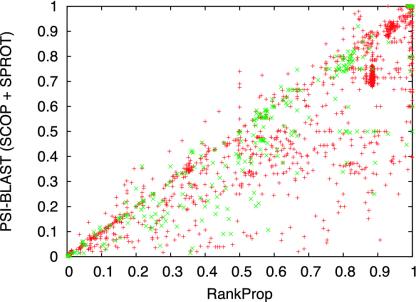
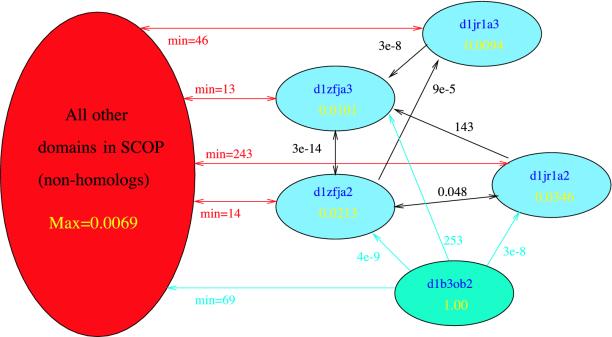
The experimental results, summarized in Fig. 2, show the relative improvements offered by the various algorithms. Even when using the small SCOP database, the psi-blast protein similarity network improves significantly upon the network created using the simpler blast algorithm: psi-blast yields better performance than blast for 51.3% of the test queries, and worse performance for only 8.2% of the queries. psi-blast benefits from the availability of a larger sequence database: increasing the database size by adding the SWISS-PROT database yields an additional improvement of the same magnitude (50.9% and 11.4%, respectively). Finally, running rankprop on the larger protein similarity network defined by psi-blast yields improved rankings for 55.3% of the queries, and decreases performance on only 9.7%. All of these differences are statistically significant at P = 0.01 according to a Wilcoxon signed-rank test. A comparison of psi-blast and rankprop ROC scores by query is shown in Fig. 3, and a diagram illustrating how rankprop successfully re-ranks homologs of a single query is shown in Fig. 4.

Fig. 2.

Relative performance of protein ranking algorithms. The graph plots the total number of test set SCOP queries for which a given method exceeds an ROC₅₀ score threshold. ROC₅₀ is the area under a curve that plots true-positive rate as a function of false-positive rate, up to the 50th false-positive. In the plot, the lower three series correspond to the three protein similarity networks described in the text; the upper series is created by running rankprop on the larger psi-blast network. For these data, the mean ROC₅₀ for the four methods are 0.506 (blast), 0.566 [psi-blast (SCOP)], 0.618 [psi-blast (SCOP plus SPROT)], and 0.707 (rankprop).

Fig. 3.

Scatter plot of ROC₅₀ scores for psi-blast versus rankprop. The plot contains 2,899 points, corresponding to all queries in the test set. Green points correspond to query domains that lie on the same protein with another domain in the test set. All other queries are red.

Fig. 4.

Visualization of part of the similarity network. Shown is a small part of the protein similarity network, where d1b30b2 is the query, and the domains are represented by light blue nodes are its homologs. The large red node represents all other domains. The cyan-colored edges from the query to other nodes are labeled with weights equal to the psi-blast E value, given d1b30b2 as the query. The rest of the edges indicate the similarity network which is formed of psi-blast E values, as described in the text. Black edges are between homologs, and red edges are between all nonhomologs and a single homolog, with the minimum E value across all nonhomologs given as the weight of the edge. No edge is drawn if psi-blast did not assign an E value. psi-blast only correctly identifies two homologs, d1zfja2 and d1jr1a2. Although d1zfja3 is assigned an E value (of 253), this assignment is larger than three of the nonhomologs in SCOP. The yellow scores inside the nodes are the rankprop activation levels (y_i values). In this case, rankprop places all of the homologs at the top of the ranked list. This assignment occurs because there are very low E value paths (by traversing edges with not more than an E value of 9e-5) between the query and all homologs, whereas even the “nearest” nonhomologs are sufficiently far away (never closer than an E value of 13 to a homolog). Note that d1jr1a2 is assigned a higher score by rankprop than d1zfja2, even though the E values assigned by psi-blast (although similar) indicate the opposite. This result is because d1zfja2 has much lower weighted edges to nonhomologs, and thus receives more of the nonhomologs' activation level (which are close to 0). Overall, the rankprop ranking gave an ROC₅₀ score of 1, whereas psi-blast gave an ROC₅₀ score of 0.78 on this query.

Note that there is some obvious structure in Figs. 2 and 3. The steep slope in the rankprop plot (Fig. 2) at around 0.9 ROC₅₀ corresponds to queries mostly from the largest superfamily in the database, the immunoglobulins with 623 proteins. These queries are also visible as a cluster at around (0.9, 0.7) in Fig. 3. rankprop's improved rankings for these queries suggests that the algorithm successfully exploits cluster structure in the protein similarity network.

rankprop is not misled by the presence of multidomain proteins in the database. Previous network-based protein similarity detection algorithms explicitly deal with multidomain proteins. For example, the intermediate sequence search algorithm (6) includes a step that extracts the region of the target sequence that matched the query and then recalculates the statistical significance of that region with respect to the target sequences. This step prevents the algorithm from inferring a false relationship between protein domains A and B through an intermediate protein containing both A and B. rankprop delivers excellent performance, even when the database contains ≈100,000 full-length proteins, many of which contain more than one domain. Furthermore, Fig. 3 shows that rankprop generally performs better than psi-blast, even when the SCOP query domain lies on the same protein as another domain in the test set. A closer investigation (see supporting information) reveals that rankprop does indeed rank these transitive domains higher than would be expected by chance. However, in general, as long as the query sequence is connected to many other proteins, then the true relationships will be mutually reinforcing during network propagation.

A well known problem with psi-blast is the occasional case in which it mistakenly pulls in a false-positive match during an early iteration. This false-positive may then pull in more false-positives in subsequent iterations, leading to corrupted results. Among the test set queries, there are 139 queries for which the psi-blast ROC₅₀ score is worse than the corresponding blast score, indicating that iteration hurt the performance of the algorithm. For these queries, rankprop outperforms blast in 106 cases, despite using as input a protein similarity network defined by psi-blast. Furthermore, the degree of improvement produced by rankprop relative to blast is often large, with a difference in ROC₅₀ >0.1 for 71 of the 106 queries (see supporting information).

Among the 282 queries for which psi-blast produces a better ranking than rankprop, most of the differences in ROC are small. There are, however, 20 queries for which psi-blast produces an ROC₅₀ that is >0.1 greater than rankprop's ROC₅₀, and one query for which the difference is >0.2 (see supporting information). Some of these queries belong to SCOP class 3 (α-β proteins), which contains a number of homologous Rossmann folds. In these cases, the first false-positives may in fact be true-positives. For the other queries, rankprop's difficulty likely arises from overpropagation through the protein similarity network. Lowering the parameter α could potentially fix this problem, because as α → 0, we obtain the same ranking as psi-blast.

Finally, the results indicate that rankprop does not spoil good initial rankings. Indeed, there is only one query for which psi-blast produces an ROC₅₀ score of 1 (a perfect ranking) and rankprop produces a score worse than 0.98. This query is the C-terminal fragment of DNA topoisomerase II, with an ROC₅₀ of 0.93. Conversely, there are 30 queries for which psi-blast has an ROC₅₀ <0.93 and rankprop produces a perfect ranking.

To better understand the source of rankprop's improvement relative to the underlying psi-blast protein similarity network, we performed an additional round of experiments using two variants of the rankprop algorithm. Each algorithmic variant restricts rankprop to a subset of the protein similarity network. In the first variant, rankprop sees only the local network structure: the target sequences that are linked directly to the query, plus the pairwise relationships among those sequences. This network of local relationships yields rankprop performance almost identical to psi-blast (see supporting information). The second variant includes nonlocal edges but eliminates all weak edges, with E values >0.005. In contrast with the previous variant, this version of the algorithm performs only slightly worse than rankprop trained using the entire network. This result indicates that the improvement of rankprop over psi-blast results primarily from rankprop's ability to learn from nonlocal network structure, and that the weak links in the network are of secondary importance. Data sets and FASTA files are available from the web site of J.W., which can be accessed at www.kyb.tuebingen.mpg.de/bs/people/weston/rankprot/supplement.html.

Discussion

rankprop is efficient enough to employ the algorithm as part of a web-based search engine. The precomputation of the psi-blast protein similarity network is clearly computationally expensive; however, this operation can be performed in advance offline. Computing the ranking with respect to a given query requires first running psi-blast with the query sequence (unless it is already in the network), and then propagating scores from the query through the network. In the experiments reported here, the propagation (20 iterations of rankprop) took on average 73 seconds to compute using a Linux machine with an Advanced Micro Devices (Sunnyvale, CA) MP 2200+ processor. blast and psi-blast take ≈21 and 331 sec per query respectively on the same database (SCOP plus SPROT). The propagation time scales linearly in the number of edges in the network. The propagation time could be improved by removing weak edges from the protein similarity network [at a relatively small cost in accuracy (see supporting information)], by running the propagation in parallel, and by reducing the number of iterations. Finally, the initial query psi-blast computation may be replaced with blast at a relatively small cost in accuracy (see supporting information), resulting in a query procedure that is faster than running a single psi-blast query on the entire database.

The experiments described here were performed by using a single set of psi-blast parameters. These parameters were previously selected by means of extensive empirical optimization using the SCOP database as a gold standard and ROC_n scores as the performance metric (17). However, even if better psi-blast parameters were available, the resulting improved E values would likely lead to a similar improvement in the performance of the rankprop algorithm.

The results reported here are given in terms of the ROC₅₀ performance measure. One might argue that a stricter (or looser) threshold might be more appropriate, depending on the cost associated with false-positives. Further experiments (see supporting information) show that rankprop continues to significantly outperform psi-blast even for relatively small values of the ROC threshold (ROC₅ or ROC₁₀). At the most strict threshold, ROC₁ (which is equivalent to the percentage of positive examples appearing before the first negative example in the ranked output), the difference between the two algorithms is no longer statistically significant. However, by using the ROC₁ measure, rankprop performs better on smaller superfamilies using a small σ, and vice versa. Therefore, a simple modification to the algorithm, in which the value of σ depends on the number of strong matches to the query sequence, once again yields strong performance relative to psi-blast. In future work, we plan to investigate more thoroughly algorithms that choose σ dynamically based on the local density of the protein similarity network.

A valuable component of the psi-blast algorithm is its method for estimating statistical confidence, in the form of E values. Currently, rankprop does not produce E values; however, approximate E values may be derivable by means of interpolation and smoothing of the psi-blast E values with respect to the rankprop ranking. Alternatively, it may be possible to fit a probability distribution to the output scores (24). This fitting will be the subject of future research.

The primary outcome of this work is not the rankprop algorithm per se, but the observation that exploiting the entire structure of the protein similarity network can lead to significantly improved recognition of pairwise protein sequence similarities. rankprop provides an efficient, powerful means of learning from the protein similarity network; however, other network-based algorithms may also yield similar improvements relative to the ranking induced by the underlying protein similarity network. Furthermore, this observation is applicable to a wide range of problem domains, including image and text ranking, as well as protein or gene ranking using different (or multiple) types of biological data.